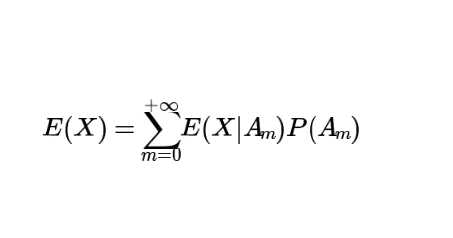L’objectif de cet article est de découvrir la notion d’espérance conditionnelle, qui peut être très utile dans certains exercices. Elle peut être retrouvée dans des sujets types EML ou EDHEC. Cet article se limite à l’étude de l’espérance conditionnelle pour les variables aléatoires réelles. L’étude de l’espérance conditionnelle pour les variables aléatoires discrètes est bien au-delà du programme.
Définition
L’espérance conditionnelle d’une variable aléatoire réelle donne la valeur moyenne de cette variable quand un certain événement est réalisé. L’espérance de la variable aléatoire \(X\) conditionnée par l’événement \(B\) se note \(E(X|B)\). On peut également définir l’espérance conditionnelle d’une variable aléatoire \(X\) par rapport à une autre variable aléatoire \(Y\), on notera de même \(E(X|Y)\).
Soit \(X\) une variable aléatoire discrète, on note \(X(\Omega)={x_k}\) avec \(k\) un entier naturel.
Si \(B\) est un événement de probabilité non nulle, sous réserve d’absolue convergence, on appelle « espérance conditionnelle de \(X\) » : \(E(X|B)=\displaystyle \sum_{k=0}^{+\infty}
x_kP_B(X=x_k)\)
Formule de l’espérance totale
Connaître l’espérance conditionnelle d’une variable aléatoire peut nous permettre de trouver son espérance.
Soit \(X\) une variable aléatoire discrète, on note \(X(\Omega)={x_k}\) avec \(k\) un entier naturel.
Soit \({A_m}\) avec \(m \in \mathbb{N}\) un système complet d’événement de \(\Omega\) tel que \(\forall m \in
\mathbb{N}, P(A_m) \le 0\)
Alors, \(X\) admet une espérance si et seulement si la série \(\displaystyle \sum_{m=0}^{+\infty}
E(X|A_m)P(A_m)\) converge absolument. Dans ce cas, on a \(E(X)=\displaystyle \sum_{m=0}^{+\infty}
E(X|A_m)P(A_m)\)
Démonstration
\(\begin{align}
E(X) \; \text{existe} & \Leftrightarrow \sum_{n \ge 0} x_nP(X=x_n) \; \text{converge absolument} \\
&\Leftrightarrow \sum_{n \ge 0} x_n(\sum_{m \ge 0} P(A_m)P_{A_m}(X=x_n) ) \;\text{converge absolument} \\
&\Leftrightarrow \sum_{n \ge 0} \sum_{m \ge 0} x_nP(A_m)P_{A_m}(X=x_n) \; \text{converge absolument}\\
&\Leftrightarrow \sum_{m \ge 0} \sum_{n \ge 0} x_nP_{A_m}(X=x_n)P(A_m) \; \text{converge absolument} \\
&\Leftrightarrow \sum_{m \ge 0} E(X|A_m)P(A_m) \;\text{converge absolument}
\end{align}\)
Ainsi en cas d’absolue convergence, on retrouve bien : \(E(X)=\displaystyle \sum_{m=0}^{+\infty}
E(X|A_m)P(A_m)\)
Propriétés
1 – L’espérance conditionnelle est linéaire : Soit \((a,b)\) un couple de réel et soit \((X,Y)\) un couple de variables aléatoires réelles. Soit \(B\) un événement. \(E(aX+bY|B)=aE(X|B)+bE(Y|B)\)
Démonstration
Soit \(X\) une variable aléatoire réelle, \(a\) un réel et \(B\) un événement de probabilité non nulle. \(E(aX|B)=\displaystyle \sum_{k=0}^{+\infty}
ax_kP_B(X=x_k)=a\displaystyle \sum_{k=0}^{+\infty}
x_kP_B(X=x_k)=aE(X|B)\)
2 – Si \(X\) est indépendant de l’événement \(B\), alors \(E(X|B)=E(X)\)
Démonstration
Soit \(X\) une variable aléatoire réelle et \(B\) un événement de probabilité non nulle tel que \(X\) et \(B\) soient indépendants. \(E(X|B)=\displaystyle \sum_{k=0}^{+\infty}
x_kP_B(X=x_k)=\displaystyle \sum_{k=0}^{+\infty}
x_kP(X=x_k)=E(X)\)
3 – L’espérance conditionnelle est croissante : si \(X\le Y\), alors \(E(X|B) \le E(Y|B)\)
Exemple avec un dé
On lance un dé équilibré à six faces. On considère deux variables aléatoires \(A\) et \(B\) telles que \(A\) vaut \(1\) quand le résultat du lancer est pair (\(A(\Omega)=(2,4,6)\)) et \(0\) sinon. \(B\) vaut \(1\) quand le résultat est un nombre premier \((B(\Omega)=(2,3,5))\) et \(0\) sinon.
L’espérance (non conditionnelle) de \(A\) vaut \(E(A)=\frac{3}{6}=\frac{1}{2}\)
L’espérance de \(A\) conditionnée à l’événement \([B=1]\) vaut \(E(A|B=1)=(1+0+0)/3=1/3\)
L’espérance de \(B\) conditionnée à l’événement \([A=0]\) vaut \(E(B|A=0)=(0+1+1)/3=2/3\)
Exemple avec des lois classiques
On lance un dé équilibré, le résultat est une variable aléatoire \(X\). \(X \hookrightarrow
\mathcal{U}([\![1,6]\!])\). On pose alors \(Y \hookrightarrow
\mathcal{U}([\![1,X]\!])\). Déterminons \(E(Y)\).
\(E(Y)=\displaystyle \sum_{n=1}^{6}E(Y|X=n)P(X=n)=\displaystyle \sum_{n=1}^{6}\displaystyle \sum_{k=1}^{n}kP_{X=n}(Y=k)P(X=n) =\displaystyle \sum_{n=1}^{6}\displaystyle \sum_{k=1}^{n} k\frac{1}{n}\frac{1}{6}=\displaystyle \sum_{n=1}^{6} \frac{1}{6n}\frac{n(n+1)}{2}=\frac{27}{12}\).
Pour plus de ressources de mathématiques, tu peux cliquer ici !