Je te présente dans cet article des polynômes hors programme : les polynômes d’Hermite. Cette suite de polynômes a été nommée en l’honneur du mathématicien Charles Hermite. Elle apparaît dans de nombreux champs d’application : physique, analyse numérique, probabiliste, dans le cas de matrices aléatoires… Les possibilités sont nombreuses et il est ainsi probable que les concepteurs de sujets de concours ou d’oraux introduisent un jour ces fameux polynômes. Cet article te présentera donc les propriétés essentielles de ces polynômes. Tu trouveras également des idées de démonstration de certaines de ces propriétés.
Définition des polynômes d’Hermite
La définition la plus courante en mathématiques est la suivante : \[\forall x \in \mathbb{R}, \forall n \in \mathbb{N}, H_n : x \mapsto (-1)^n \phi^{(n)}(x) \times \frac{1}{\phi(x)}\]
On peut également écrire cette suite de fonction sous forme de développement polynomial. Ainsi,
\[\forall x \in \mathbb{R}, \forall n \in \mathbb{N}, H_n(x) = \displaystyle \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} (-1)^k \frac{n!}{2^kk!(n – 2k)!}x^{n – 2k}\]
Propriétés des polynômes d’Hermite
Première relation de récurrence :
\( \forall n \in \mathbb{N}^*, \forall x \in \mathbb{R}, H_{n + 1}(x) = xH_n(x) – nH_{n – 1}(x)\)
Seconde relation de récurrence :
\( \forall n \in \mathbb{N}^*, \forall x \in \mathbb{R}, H_n'(x) = nH_{n – 1}(x)\)
Résultats immédiats :
\( H_0(x) = 1
H_1(x) = x
H_2(x) = x^2 – 1
H_3(x) = x^3 – 3x
H_4(x) = x^4 – 6x^2 + 3\)
Polynômes d’Hermite et orthogonalité :
\( \forall n \in \mathbb{N}, ({H_0, H_1, … , H_n)}\) est une famille orthogonale (mais pas orthonormée) de \(\mathbb{R}_n[X]\). Par conséquent, elle est libre et comme elle est de dimension \(n + 1\), il s’agit d’une base de \(\mathbb{R}_n[X]\).
Démonstrations
Première relation de récurrence
Soit \( n \in \mathbb{N}^*\), soit \(x \in \mathbb{R}\),
\( H_{n + 1}(x) = (-1)^{n + 1} \frac{\phi^{(n + 1)}(x)}{\phi(x)} \)
\(H_{n + 1}(x) = (-1)^{n + 1} \times \frac{1}{\phi(x)} (\phi’)^{(n)}(x) \)
\(H_{n + 1}(x) = (-1)^{n + 1} \times \frac{1}{\phi(x)} \left( – x e^{(- \frac{x^2}{2})} \right)^{(n)}\)
\(H_{n + 1}(x) = (-1)^{n + 1} \times \frac{1}{\phi(x)} \left( \displaystyle\sum_{k=0}
^n {{n}\choose{k}} (-x)^k (e^{- \frac{x^2}{2}})^{(n-k)} \right) \)
\(H_{n + 1}(x) = (-1)^{n + 1} \times \frac{1}{\phi(x)} \left( -x \phi^{(n)}(x) – n \phi^{(n – 1)}(x) + 0 + … + 0 \right) \)(d’après la formule de Leibniz)
\(H_{n + 1}(x) = -x \frac{(-1)^{n + 1}}{\phi(x)}\phi^{(n)}(x) – n (-1)^{n + 1}\times \frac{1}{\phi(x)}\phi^{(n – 1)}(x)\)
\(H_{n + 1}(x) = x \frac{(-1)^{n}}{\phi(x)}\phi^{(n)}(x) – n \frac{(-1)^{n – 1}}{\phi(x)}\phi^{(n – 1)}(x)\)
\(\fbox{\(H_{n + 1}(x) = xH_n(x) – nH_{n-1}(x)\)}\)
Seconde relation de récurrence
\( \forall n \in \mathbb{N}^*, \forall x \in \mathbb{R}, \\
\phi(x) H_n(x) = (-1)^n \phi^{(n)}(x)\)
\(\phi'(x)H_n(x) + \phi^{(n)}(x)H_n'(x) = (-1)^n\phi^{(n + 1)}(x)\) (en dérivant)
\(- \ x \phi(x) H_n(x) + \phi(x)H_n'(x) = (-1)^n\phi^{(n + 1)}(x)\)
\(- \ xH_n(x) + H_n'(x) = \ – \frac{(-1)^{(n + 1)}}{\phi(x)}\phi^{(n + 1)}(x)\)
\(-\ xH_n(x) + H_n'(x) = \ – H_{n + 1}(x)\)
\(- \ xH_n(x) + H_n'(x) = \ – xH_{n}(x) + nH_{n_1}(x)\)
\(\fbox { \(H_n'(x) = nH_{n_1}(x)\)}\)
Polynômes d’Hermite et orthogonalité
Soient \((i ; j) \in \mathbb{N}^2\) avec \( i < j\).
\( < H_i; H_j > \ = \displaystyle \int_{-\infty}^{+\infty} H_i(t)H_j(t)\phi(t) \, \mathrm{d}t \)
\(< H_i; H_j > \ = \displaystyle \int_{-\infty}^{+\infty} H_i(t) (-1)^j\phi^{(j)}(t)\, \mathrm{d}t \)
En posant \( u(t) = H_i(t) \) et \(v'(t) = (-1)^j\phi^{(j)}(t)\), on a \(u'(t) = iH_{i – 1}(t)\) et \(v(t) = (-1)^j\phi^{(j – 1)}(t)\).
\( < H_i; H_j > \ = [H_i(t)(-1)^j\phi^{(j – 1)}(t)]_{-\infty}^{+\infty} – \displaystyle \int_{-\infty}^{+\infty}iH_{i – 1}(t)(-1)^j\phi^{(j)}(t)\, \mathrm{d}t \)
\( < H_i; H_j > \ = [-\phi(t)H_{j – 1}H_i(t)]_{-\infty}^{+\infty} + i\displaystyle \int_{-\infty}^{+\infty}H_{i – 1}(t)H_{j – 1}(t)\phi(t)\, \mathrm{d}t \)
Or, \( < H_i; H_j > \ = [-\phi(t)H_{j – 1}H_i(t)]_{-\infty}^{+\infty} = 0 \)
et \(\displaystyle \int_{-\infty}^{+\infty}H_{i – 1}(t)H_{j – 1}(t)\phi(t)\, \mathrm{d}t = \ < H_{i – 1}; H_{j – 1}>\).
Donc, pour \((i ; j) \in \mathbb{N}^2\) avec \( i < j\),
\( < H_i; H_j > \ = i < H_{i – 1}; H_{j – 1}>\)
\( < H_i; H_j > \ = i (i – 1) < H_{i – 2}; H_{j – 2}>\)
D’où \( < H_i; H_j > \ = i! < H_{0}; H_{j – i}>\) par itérations successives.
On obtient alors :
\( < H_i; H_j > \ = i! \displaystyle \int_{-\infty}^{+\infty}H_{0}(t)H_{j – i}(t)\, \mathrm{d}t\)
\( < H_i; H_j > \ = i! \displaystyle \int_{-\infty}^{+\infty} 1 \times (-1)^{j – i}\phi^{(j – i)}(t)\, \mathrm{d}t\)
\( < H_i; H_j > \ = i! (-1)^{j – i} [\phi^{(j – i – 1)}(t)]_{-\infty}^{+\infty}\)
\( < H_i; H_j > \ = i! (-1)^{j – i} [\frac{1}{(-1)^{(j – i – 1)}}H_{j – i – 1}(t) \phi(t)]_{-\infty}^{+\infty}\)
Soit finalement \( < H_i; H_j > \ = 0\).
Donc, la famille \(({H_0, H_1, … , H_n)}_{n \ge 0}\) est une famille orthogonale de \(\mathbb{R}[X]\).
On pourrait également montrer que \(\forall k \in \mathbb{N}, deg H_k = k\).
Donc, \(\forall n \in \mathbb{N}, ({H_0, H_1, … , H_n)}\) est une famille orthogonale de \(\mathbb{R}_n[X]\), donc libre et c’est une base.
Cette famille n’est en revanche pas orthonormée.
Après calculs, on trouve que \(\|H_0\| = (2\pi)^{\frac{1}{4}}\).
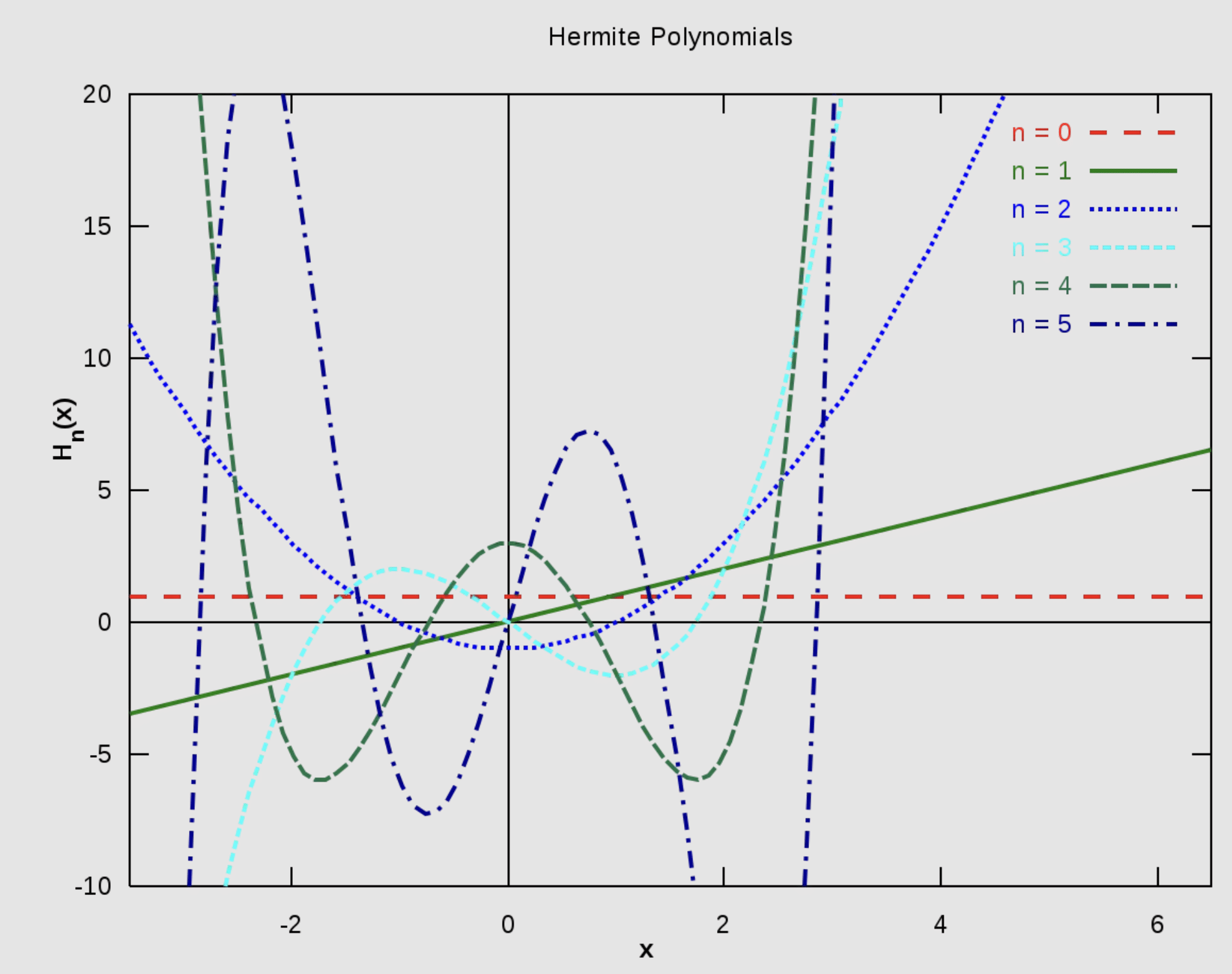
Représentation graphique des polynômes d’Hermite
Le schéma ci-dessous représente graphiquement les premiers polynômes d’Hermite :
Sujet de concours avec la notion des polynômes d’Hermite
J’espère que cet article t’a plu et qu’il a pu t’éclairer sur le sujet. N’hésite pas à aller consulter nos autres articles en cliquant ici !