Major Prépa > Académique > Python > Les scripts ultra-classiques à savoir faire en Python

Il existe une variété de scripts extrêmement classiques qui revenaient déjà en boucle à l’époque de Scilab et qui vont continuer d’apparaître fréquemment en Python dans les sujets. Voici une liste (non exhaustive) de scripts qu’il te faut maîtriser parfaitement. Ces scripts sont principalement des scripts de recherche de solution(s), car ce sont les plus fréquents aux concours et ils reviennent sous différentes formes.
La recherche de solution
Le balayage
Explication du code
On veut résoudre \(f(x) = k\) dans l’intervalle \([a,b]\), en trouvant une solution approchée à \(e\) près.
Ici, on va calculer \(f(a)\) puis \(f(a+e)\), puis \(f(a+2e)\) etc., jusqu’à obtenir une image strictement supérieure à \(k\) et s’arrêter. Une fois qu’on s’est arrêté, on est sûr d’avoir une solution de notre équation, avec au maximum une erreur de \(e\).
Les encadrements
Ici aussi, un immense classique déjà présent dans EMLYON 2023 (Maths Appliquées).
Explication du code
Pour ce code, c’est même la consigne qui te semblera classique tant elle revient toujours : “Renvoyer le plus petit entier naturel \(n\) tel que \(Un > a\).”
Ici, on commence par initialiser \(U_0\), et tant que la condition n’est pas respectée, on continue d’utiliser notre relation \(U_{n+1}\)= \(f(U_n)\) en utilisant une variable compteur \(n\), pour, au final, renvoyer notre plus petit entier naturel \(n\), validant la condition à la fin.
La méthode de Newton
Explication du code
C’est de loin la méthode la plus rapide pour chercher des solutions approchées de l’équation \(f(x) = 0\) (mais donc en réalité tous types d’équations). Cette méthode peut aussi être vue comme la plus contraignante, puisqu’elle nécessite de remplir deux conditions :
- \(f\) doit être dérivable sur l’intervalle considéré
- la dérivée de \(f\) ne doit pas s’annuler sur l’intervalle considéré
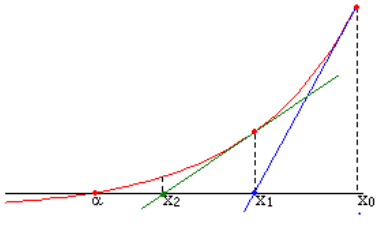
Cette méthode repose sur un fondement mathématique qu’il n’est pas aisé de retranscrire à l’écrit, puisqu’il se base sur les tangentes de notre fonction \(f\).
Il s’agit de trouver une première tangente à \(Cf\) au point \(x_0\), puis de prendre le point d’intersection \(x_1\) entre cette tangente et l’axe des abscisses. Ensuite, on itère ce processus par récurrence et on se rapproche ainsi mécaniquement de la solution de \(f(x) = 0\).
N.B. : Il est possible de remplacer la boucle for par une boucle while pour avoir une condition d’arrêt précise si besoin.
Voici une représentation graphique de cette méthode :
Les algorithmes de tri
Explication du code
On commence par écrire un script pour regarder si notre liste est triée ou non (on peut en réalité l’intégrer dans le tri liste, mais c’est plus clair ainsi). Ensuite, on trie la liste tant qu’elle n’est pas triée.
Pour ce faire, dès que l’on observe que terme \(n-1\) est plus grand que le terme \(n\), on met l’un à la place de l’autre. Ainsi, on se retrouve toujours in fine avec une liste parfaitement triée.
La recherche dichotomique
L’algorithme de dichotomie
La dichotomie permet de dire si oui ou non un élément \(v\) est dans une liste \(L\), et c’est un grand classique des concours. Tu peux même le retrouver dès maintenant dans le sujet Ecricome 2023 (Maths Appliquées).
Explication du code
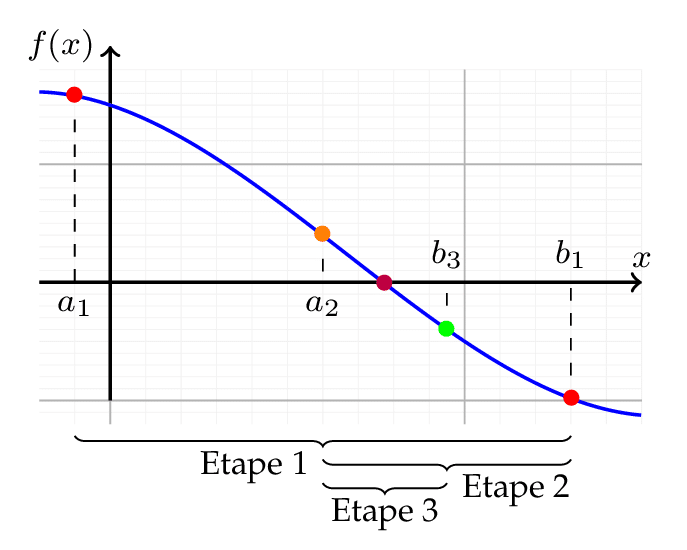
On commence par entrer une fonction \(f\) définie sur un intervalle \( [a,b] \) tel que \(f(a)\) et \(f(b)\) soient de signes opposés. On prend ensuite le milieu de l’intervalle.
Tout va ici reposer sur la règle des signes, qui nous dit que la multiplication de deux nombres de mêmes signes donne quelque chose de positif. Et inversement, que la multiplication de deux nombres de signes contraires donne quelque chose de négatif.
Ainsi, si \(f(a)\) et \(f(m)\) sont de signes contraires, la solution se situe alors dans l’intervalle \([a,m]\) (puisqu’un point se situe au-dessus de l’axe des abscisses et l’autre en dessous), et sinon, elle se situe dans l’intervalle \([m,b]\). Ainsi, la dichotomie est souvent plus rapide que le balayage, car on coupe à chaque fois l’intervalle en deux, alors que le balayage part d’une extrémité de l’intervalle.
Puisqu’à chaque fois, on coupe l’intervalle en deux en se rapprochant toujours plus du point \( f(x)=0 \), on finit par l’atteindre avec la précision souhaitée.
Les scripts de conversion
Matrice en liste
Explication du code
Ce code sert à transformer la matrice d’adjacence d’un graphe en sa liste de listes d’adjacence.
Une boucle externe itère sur les indices des lignes de la matrice, allant de \(0\) à \(p-1\). À chaque itération de la boucle externe, une liste vide \(V\) est créée pour stocker les indices des éléments non nuls de la ligne en cours. Une boucle interne itère sur les indices des colonnes de la matrice, allant de \(0\) à \(n-1\).
Pour chaque élément de la matrice à l’intersection de la ligne \(i\) et de la colonne \(j\), on vérifie si l’élément est différent de zéro. Si l’élément est non nul, l’indice de la colonne \(j\) est ajouté à la liste \(V\). Une fois que la boucle interne a parcouru toutes les colonnes de la ligne en cours, la liste \(V\) est ajoutée à la liste principale \(L\).
Le processus se répète pour chaque ligne de la matrice, ajoutant toutes les listes \(V\) correspondant à chaque ligne à la liste principale \(L\). Une fois que toutes les itérations sont terminées, la liste \(L\) contenant toutes les sous-listes (les indices des éléments non nuls de chaque ligne) est renvoyée en sortie de la fonction.
On a donc bien créé une liste d’adjacence à partir d’une matrice d’adjacence.
N.B. : Une liste d’adjacence d’un graphe est une liste de \(n\) listes (\(n\) étant l’ordre du graphe), où la i-ème liste contient la liste des sommets adjacents au sommet \(i\).
Ce procédé de conversion est très commun lorsqu’on travaille sur les graphes en Python. Par exemple sur l’algorithme de Dijkstra, et sera donc certainement un classique des concours.
Liste en matrice
Explication du code
Ce code sert à transformer la liste d’adjacence d’un graphe en sa matrice d’adjacence. On commence par initialiser une matrice pleine de zéros. Ensuite, la double boucle sert à parcourir toutes les sous-listes de \(L\) (c’est-à-dire chaque élément de \(L\), les éléments étant eux-mêmes des listes).
Au fur et à mesure de ce parcours, la fonction met à \(1\) les éléments correspondants dans la matrice \(A\), en utilisant les indices fournis dans chaque sous-liste. Cela permet de reconstruire la matrice originale à partir de sa représentation sous forme de liste de listes.
Conclusion
Ces algorithmes sont véritablement de grands classiques des concours et tu te dois de les connaître et de les comprendre. Une fois que tu les auras bien compris, ils seront une source de points très faciles et rapides à aller chercher.
Tu peux également retrouver toutes nos autres ressources mathématiques ici.