Cet article te propose 10 astuces sur les sommes, expliquées comme tu ne l’as jamais vu ! Celui-ci, d’un niveau avancé, s’adresse aux cubes qui souhaitent approfondir le programme de maths dans les détails (afin d’en avoir une parfaite compréhension), ou aux carrés les plus téméraires.
Compatible maths approfondies (voire maths appliquées).
Tu peux aussi consulter nos autres astuces sur les sommes pour des niveaux moins avancés :
10 astuces sur les sommes – niveau débutant
8 astuces sur les sommes – niveau intermédiaire
1) Généralisation de la somme des \(1\)
Soit \(E\) un ensemble non vide.
Que vaut la somme : \(\displaystyle \sum_{k \in E}1\) ?
Attention, là ça ne rigole plus, on rentre dans du très très théorique… Et pourtant, c’est si simple pour celui qui connaît son cours sur le bout des doigts…
Pour trouver la valeur de cette somme, il suffit de connaître combien il y a d’éléments dans cette somme. Or, il s’avère qu’en maths, nous possédons un opérateur pour compter les éléments (même dans les cas les plus abstraits) : il s’agit du cardinal !
Il est logique de dire que le nombre d’éléments de l’ensemble \(E\) est donc \(\text{card}E\).
Donc : \(\displaystyle \sum_{k \in E}1=\text{Card}(E)\)
Bonus : que vaut \(\displaystyle \sum_{k \in \mathcal{P}(E)}1\) ?
Spéciale dédicace à mon cher Christian Skiada qui m’a tout appris sur cette somme dès les premières minutes de son tout premier cours.
Bonus, car à la limite du programme, étant donné que le dénombrement ne fait plus vraiment partie du cours. En suivant la même logique, il faut savoir le nombre d’éléments de l’ensemble des parties de \(E\) \(\mathcal{P}(E)\). Cet ensemble reste au programme de 2021 (alors que le dénombrement, non), on donnera quand même son cardinal mais on ne le démontrera plus, à savoir : \(\text{Card}(\mathcal{P}(E))=2^{\text{Card}(E)}\)
Donc, finalement : \(\displaystyle \sum_{k \in \mathcal{P}(E)}1=2^{\text{Card}(E)}\)
2) Reconnaître les sommes les plus classiques
Voilà une liste des sommes les plus classiques (quasiment toutes hors-programme, donc elles te seront toutes données en résultats préliminaires ou tu auras à les démontrer au préalable au moins).
· Pour la somme \(\displaystyle \sum_{k}{{n}\choose{k}}\), penser à la formule du binôme de Newton.
· Pour la somme \(\displaystyle \sum_{k=n}^{p}{{k}\choose{n}}={{p+1}\choose{n+1}}\), il s’agit de la formule de Pascal itérée (elle peut se démontrer par récurrence).
· Pour la somme \(\displaystyle \sum_kk \dots {{n}\choose{k}}\), penser à faire la « petite formule » (celle qui permet de diminuer le coefficient binomial d’un rang), puis la formule du binôme de Newton.
· Pour la somme \(\displaystyle \sum_kk \dots {{k}\choose{n}}\), penser de même à faire la « petite formule », puis terminer avec la formule de Pascal itérée.
· Pour la somme \(\displaystyle \sum_{k=0}^m \frac{1}{{n}\choose{k}}{{m}\choose{k}}\), penser à faire une manipulation sur les coefficients binomiaux de sorte à se ramener à la formule de Pascal itérée.
· Pour la somme \(\displaystyle \sum_{k} {{n}\choose{k}}{{n-k}\choose{p-k}}\), penser à faire une manipulation sur les coefficients binomiaux de sorte à se ramener à la formule du binôme de Newton.
· Pour la somme \(\displaystyle \sum_{k=0}^n {{p}\choose{k}}{{q}\choose{n-k}}\), il s’agit de la formule de Vandermonde. Elle se démontrait autrefois de façon combinatoire, mais désormais, elle ne se montre que de façon polynomiale.
· Pour la somme \(\displaystyle \sum_{i+j=n} {{p}\choose{i}}{{q}\choose{j}}\), il s’agit d’une variante de la formule de Vandermonde tout simplement.
On pourra donc écrire que : \(\displaystyle \sum_{k=0}^n {{p}\choose{k}}{{q}\choose{n-k}}=\sum_{i+j=n} {{p}\choose{I}}{{q}\choose{j}}={{p+q}\choose{n}}\).
· Pour la somme \(\displaystyle \sum_{k=p}^{n-q} {{k}\choose{p}}{{n-k}\choose{q}}={{n+1}\choose{p+q+1}}\), on l’appelle parfois la formule de Vandermonde « par le bas ». Honnêtement, peu de chance que tu aies à démontrer cette formule qui se fait totalement de façon combinatoire (et c’est pas la plus simple…)
3) Somme indexée par un rectangle (double somme classique)
Soient \((n,p) \in (\mathbb N^*)^2\)
Fonctionnement d’une somme double classique dont les deux indices \(i\) et \(j\) sont indépendants.
La démonstration n’est sûrement pas exigible, il s’agit juste de comprendre pour être plus à l’aise dans les calculs.
On sait que : \(S_{n,p}=\displaystyle \sum_{\scriptstyle 1\le i\le n\atop\scriptstyle 1 \le j \le n}a_{i,j}=\sum_{i=1}^n \sum_{j=1}^pa_{i,j}\)
En fait, on peut disposer les \((a_{i,j})\) dans un tableau à double entrée :
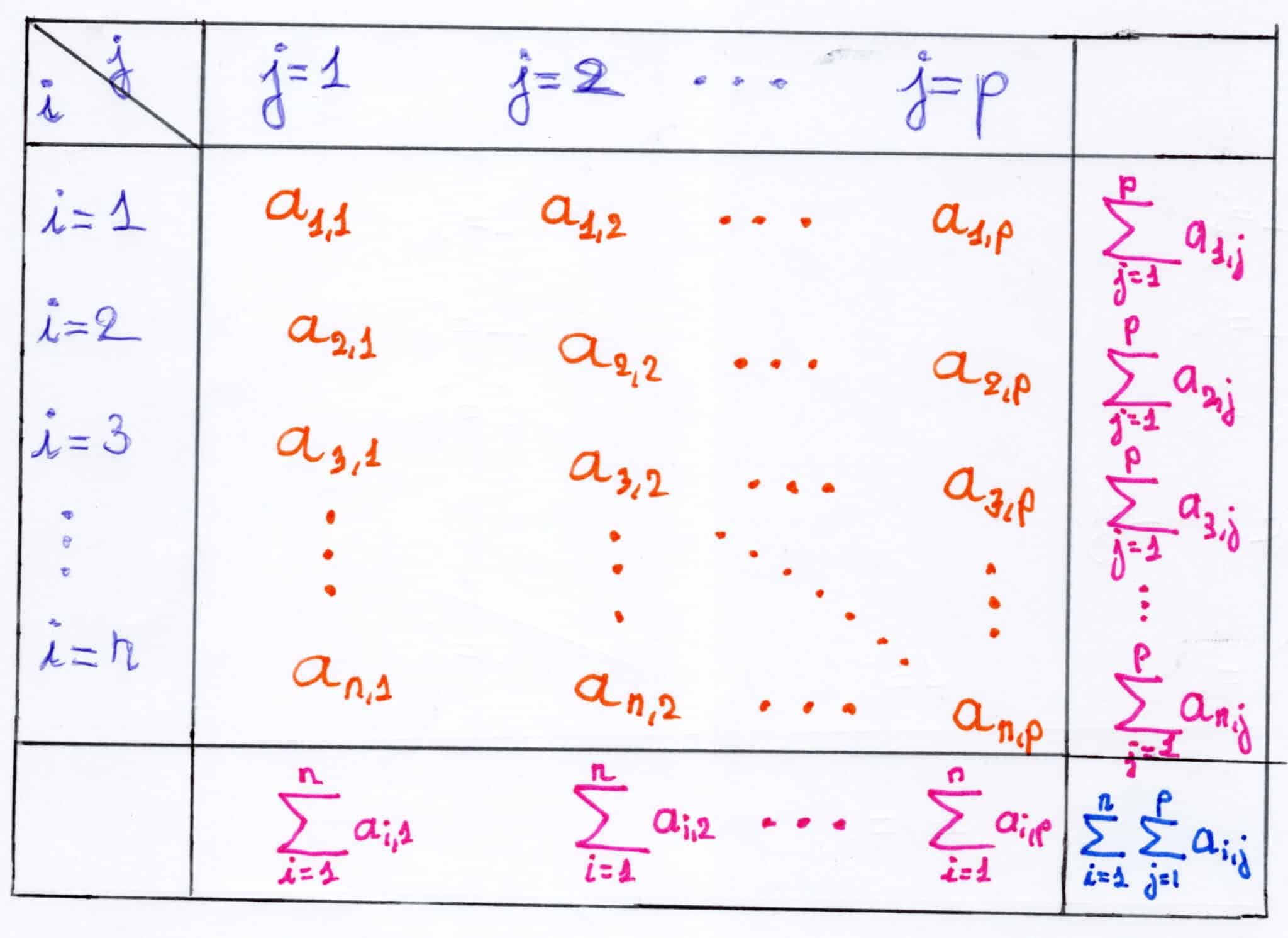
Il est intéressant de comprendre comment fonctionne cette somme plus concrètement avec un exemple.
Pour \(n=2, p=3\), on a :
\(
S_{2,3}=a_{1,1}+a_{2,1}+a_{1,2}+a_{2,2}+a_{1,3}+a_{2,3}
\)
Et en ordonnant les \((a_{i,j})\) par ordre des lignes et des colonnes du tableau :
\(
\begin{align}
S_{i,j}=&=\underbrace{a_{1,1}+a_{1,2}+a_{1,3}}_{i=1, 1 \le j \le 3}+\underbrace{a_{2,1}+a_{2,2}+a_{2,3}}_{i=2, 1 \le j \le 3} \\
&=\underbrace{\displaystyle \sum_{j=1}^3 a_{i,j}}_{i=1}+\underbrace{\displaystyle \sum_{j=1}^3 a_{i,j}}_{i=2} \\
&=\displaystyle \sum_{i=1}^2 \left( \sum_{j=1}^3 a_{i,j} \right) \\
&=\displaystyle \sum_{\scriptstyle 1\le i\le 2\atop\scriptstyle 1 \le j \le 3} a_{i,j}
\end{align}
\)
4) Somme indexée par un triangle
Soit \(n \in \mathbb N^*\)
Fonctionnement d’une somme double classique dont les deux indices \(i\) et \(j\) sont indépendants.
La démonstration n’est sûrement pas exigible, il s’agit juste de comprendre pour être plus à l’aise dans les calculs.
On sait que : \(S_n=\displaystyle \sum_{1 \le i \le j \le n}a_{i,j}=\sum_{j=1}^n \sum_{i=1}^{j}a_{i,j}=\sum_{i=1}^{n} \sum_{j=i}^na_{i,j}\)
On dispose alors les \((a_{i,j})\) dans un tableau à double entrée, en faisant toujours attention que l’indice \(i\) soit plus petit que l’indice \(j\) (\(i \le j\))

Il est intéressant de comprendre comment fonctionne cette somme plus concrètement avec un exemple.
Pour \(n=3\) :
\(
\begin{align}
S_2&=a_{1,2}+a_{2,2}+a_{1,3}+a_{3,3}+a_{2,3}+a_{1,1} \\
&=\underbrace{a_{1,1}+a_{1,2}+a_{1,3}}_{i=1, i \le j \le 3}+\underbrace{a_{2,2}+a_{2,3}}_{i=2, i \le j \le 3}+\underbrace{a_{3,3}}_{i=3, i \le j \le 3} \\
&=\displaystyle \sum_{i=1}^3\left(\sum_{i \le j \le 3}a_{i,j}\right) \\
&=\displaystyle \sum_{\scriptstyle 1\le i\le 3\atop\scriptstyle i \le j \le 3}u_{i,j} \\
&=\displaystyle \sum_{1 \le i \le j \le 3}u_{i,j}
\end{align}
\)
5) Somme double indexée par un triangle supérieur
Soit \(n \ge 2\)
Fonctionnement d’une somme double classique dont les deux indices \(i\) et \(j\) sont indépendants.
La démonstration n’est sûrement pas exigible, il s’agit juste de comprendre pour être plus à l’aise dans les calculs.
On sait que : \(S_n=\displaystyle \sum_{1 \le i < j \le n}a_{i,j}=\sum_{j=2}^n \sum_{i=1}^{j-1}a_{i,j}=\sum_{i=1}^{n-1} \sum_{j=i+1}^na_{i,j}\)
On dispose alors les \((a_{i,j})\) dans un tableau à double entrée, en faisant toujours attention que l’indice \(i\) soit plus petit que l’indice \(j\) (\(i \le j\))
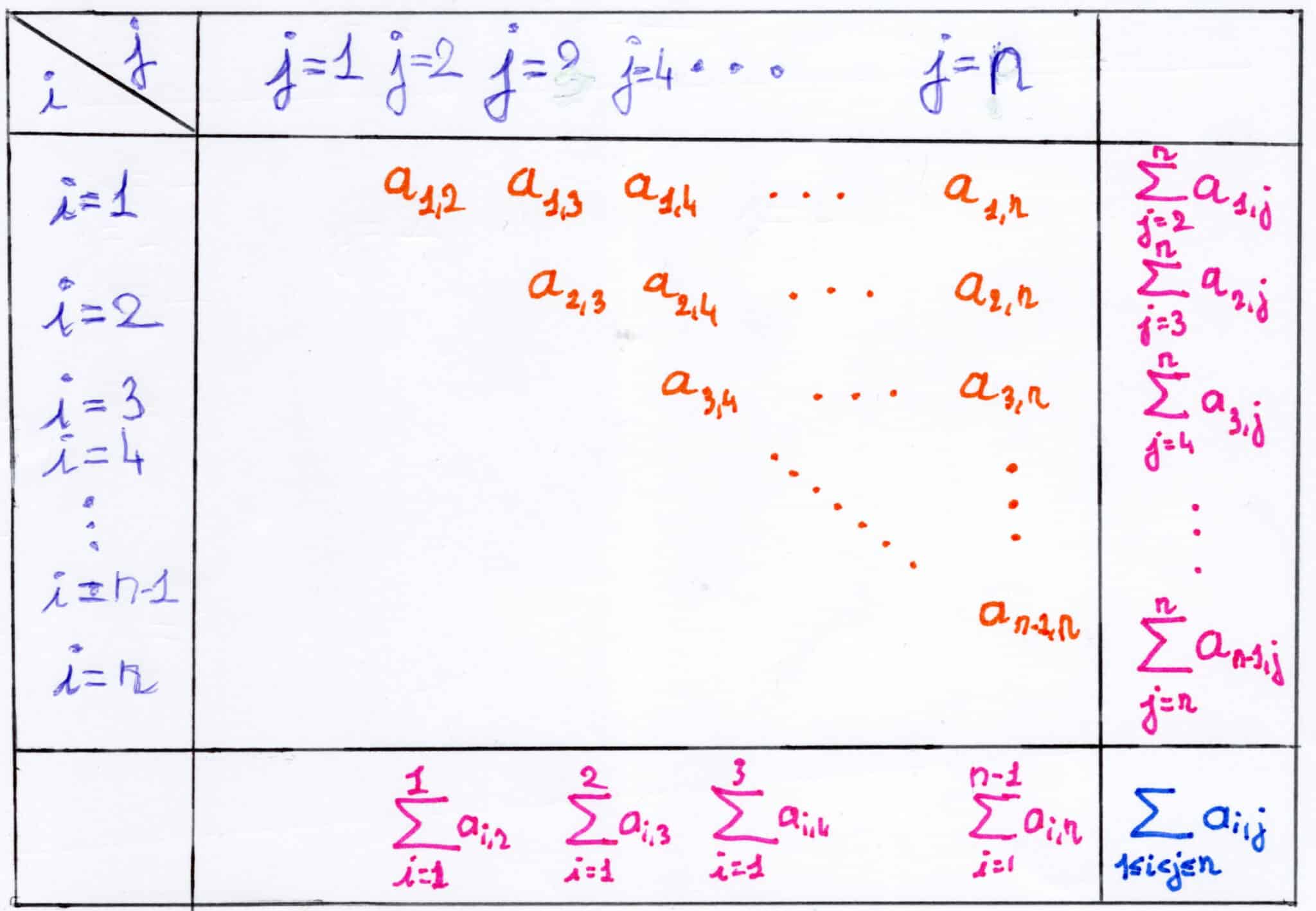
Pour \(n=4\) :
\(
\begin{align}
S_4&=a_{1,2}+a_{1,4}+a_{2,3}+a_{2,3}+a_{3,4}+a_{2,4}+a_{1,3} \\
&=\underbrace{a_{1,2}+a_{1,3}+a_{1,4}}_{\scriptstyle i=1, 2\le j\le 4 \ \text{i.e :}\atop{\scriptstyle i=1,i+1\le j\le 4 \ \text{i.e :} \atop{\scriptstyle i=1,i< j\le 4}}}+\underbrace{a_{2,3}+a_{2,4}}_{\scriptstyle i=2, 3\le j\le 4\ \text{i.e :}\atop{\scriptstyle i=2,i+1\le j\le 4 \ \text{i.e :} \atop{\scriptstyle i=2,i< j\le 4}}}+\underbrace{a_{3,4}}_{\scriptstyle i=3, 4\le j\le 4\ \text{i.e :}\atop{\scriptstyle i=3,i+1\le j\le 4 \ \text{i.e :} \atop{\scriptstyle i=3,i< j\le 4}}} \\
&=\displaystyle \sum_{i=1}^3\left(\sum_{i < j \le 4}a_{i,j}\right) \\
&=\displaystyle \sum_{\scriptstyle 1\le i\le 3\atop\scriptstyle i < j \le 4}a_{i,j} \\
&=\displaystyle \sum_{1 \le i < j \le 4}a_{i,j}
\end{align}
\)
6) Bonus : somme indexée par un carré sans sa diagonale
Maintenant que tu as compris le fonctionnement de ces sommes doubles, tu peux comprendre que cette somme :
\(\displaystyle 2\sum_{1 \le i < j \le n}a_{i,j}=\sum_{\scriptstyle 1\le i < j \le n\atop\scriptstyle 1 \le j < i \le n}a_{i,j}=\sum_{\scriptstyle (i,j) \in [\![1,n]\!]^2 \atop\scriptstyle i \ne j}a_{i,j}\)
se visualise comme un tableau à double entrée complet auquel on enlève la diagonale.
7) Nombre de termes de la généralisation de la somme double indexée par un triangle
Soient \((n,p) \in \mathbb N^2\) tels que \(p \le n \)
Attention, ici, on rentre dans du hors-programme, comme le chapitre sur le dénombrement a été supprimé en 2021.
Toutefois, il peut être intéressant de garder dans un coin de ta tête les résultats suivants (pas la peine de les apprendre par cœur, ils seront forcément admis dans l’énoncé du sujet s’ils sont nécessaires à la résolution du problème) :
– la somme \(\displaystyle \sum_{1 \le x_1 < x_2 < \dots < x_p \le n}\) contient \({{n}\choose{p}}\) termes ;
– la somme \(\displaystyle \sum_{1 \le x_1 \le x_2 \le \dots \le x_p \le n}\) contient \({{n+p-1}\choose{p}}\) termes.
Pourquoi est-il intéressant de savoir ça ? Car imagine que ces sommes sont en fait des sommes de 1, on peut écrire que :
– \(\displaystyle \sum_{1 \le x_1 < x_2 < \dots < x_p \le n}1={{n}\choose{p}}\) ;
– \(\displaystyle \sum_{1 \le x_1 \le x_2 \le \dots \le x_p \le n}1={{n+p-1}\choose{p}}\).
8) Somme indexée par une relation affine du type \(i+j=n\)
Soit \(n \in \mathbb N\)
Pourquoi \(\displaystyle \sum_{\scriptstyle (i,j) \in \mathbb N^2\atop\scriptstyle i+j=n}a_{i,j}= \sum_{i \in [\![0,n]\!]}a_{i,n-i}\) ?
Tout se passe comme si on avait posé \(j=n-i\)
Explication détaillée de cela :
\(
\{a_{i,j} \backslash (i,j) \in \mathbb N^2, i+j=n\}=\{a_{i,j} \backslash 0 \le i, 0 \le j, j=n-i\}
\)
Donc, en remplaçant dans l’ensemble tous les \(j\) par \(n-i\) :
\(
\begin{align}
\{a_{i,j} \backslash (i,j) \in \mathbb N^2, i+j=n\}&=\{a_{i,n-i} \backslash 0 \le i, 0 \le n-i\} \\
&=\{a_{i,n-i} \backslash 0 \le i, i \le n\} \\
&=\{a_{i,n-i} \backslash 0 \le i \le n\}
\end{align}
\)
Donc, \(\displaystyle \sum_{\scriptstyle (i,j) \in \mathbb N^2\atop\scriptstyle i+j=n}a_{i,j}= \sum_{i \in [\![0,n]\!]}a_{i,n-i}\)
N.-B. : Fonctionnement et comportement de l’ensemble \(\{a_{i,j} \backslash (i,j) \in \mathbb N^2, i+j=n\}\)
Si on détaille l’ensemble, on a :
\(\{a_{i,j} \backslash (i,j) \in \mathbb N^2, i+j=n\}=\{(0,n),(1,n-1),(2,n-2), \dots ,(n-1,1),(n,0)\}\)
En fait, quoi qu’il arrive, la somme de chaque couple doit toujours faire \(n\) (ce qui est logique vis-à-vis de la relation affine \(i+j=n\)).
9) Somme indexée par une relation affine du type \(i+j+k=n\) (généralisation…)
Soit \(n \in \mathbb N\)
Pourquoi \(\displaystyle \sum_{\scriptstyle (i,j,k) \in \mathbb N^3\atop\scriptstyle i+j+k=n}a_{i,j,k}= \sum_{p=0}^n \left(\sum_{\scriptstyle (i,j) \in \mathbb N^2\atop\scriptstyle i+j=n}a_{i,j,n-i-j}\right)\) ?
Tout se passe comme si on avait posé \(k=n-i-j\)
Explication détaillée de cela :
\(
\{a_{i,j,k} \backslash (i,j,k) \in \mathbb N^3, i+j+k=n\}=\{a_{i,j,k} \backslash 0 \le i, 0 \le j, 0 \le k, k=n-i-j\}
\)
Donc, en remplaçant dans l’ensemble tous les \(k\) par \(n-i-j\) :
\(
\begin{align}
\{a_{i,j,k} \backslash (i,j,k) \in \mathbb N^3, i+j+k=n\}&=\{a_{i,j,n-i-j} \backslash 0 \le i, 0 \le j, 0 \le n-i-j\} \\
&=\{a_{i,j,n-i-j} \backslash 0 \le i, 0 \le j, i+j \le n\} \\
&=\{a_{i,j,n-i-j} \backslash 0 \le i, 0 \le j, 0 \le i+j \le n\}
\end{align}
\)
D’où, en posant \(p=i+j\) :
\(
\begin{align}
\{a_{i,j,k} \backslash (i,j,k) \in \mathbb N^3, i+j+k=n\}&=\{a_{i,j,n-i-j} \backslash 0 \le i, 0 \le j, 0 \le p \le n, p=i+j\}
&=\{a_{i,j,n-i-j} \backslash 0 \le i, 0 \le j, p \in [\![0,n]\!] p=i+j\}
\end{align}
\)
Ainsi : \(\displaystyle \sum_{\scriptstyle (i,j,k) \in \mathbb N^3\atop\scriptstyle i+j+k=n}a_{i,j,k}= \sum_{p=0}^n \left(\sum_{\scriptstyle (i,j) \in \mathbb N^2\atop\scriptstyle i+j=n}a_{i,j,n-i-j}\right)\)
N.-B. : Fonctionnement et comportement de l’ensemble \(\{a_{i,j,k} \backslash (i,j,k) \in \mathbb N^3, i+j+k=n\}\)
Si on détaille l’ensemble, on a :
\(\{a_{i,j,k} \backslash (i,j,k) \in \mathbb N^3, i+j+k=n\}=\{a_{i,j,n-i-j} \backslash 0 \le i, 0 \le j, p \in [\![0,n]\!], p=i+j\} \)
\(
\begin{align}
\{a_{i,j,k} \backslash (i,j,k) \in \mathbb N^3, i+j+k=n\}=\{
&(0,0,n-0), \\
&(0,1,n-1),(1,0,n-1), \\
&(0,2,n-2),(1,1,n-2),(2,0,n-2), \\
&(0,3,n-3),(1,2,n-3),(2,1,n-3),(3,0,n-3), \\
&\dots \\
& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \dots\}
\end{align}
\)
En fait, quoi qu’il arrive, la somme de chaque \(3\)-uplet doit toujours faire \(n\) (ce qui est logique vis-à-vis de la relation affine \(i+j+k=n\)).
10) Astuce calculatoire : calculer la somme \(\displaystyle \sum_{k=1}^nk3^k\)
Soit \(n \in \mathbb N^*\)
Toute l’astuce ici réside dans le fait de faire apparaître une somme « invisible », une somme des \(1\) :
\(\forall k \in [\![1,n]\!], k=\text{Card}([\![1,k]\!])=\displaystyle \sum_{j=1}^k1\)
\(
\begin{align}
\displaystyle \sum_{k=1}^nk3^k&=\sum_{k=1}^n \text{Card}([\![1,k]\!])3^k \\
&=\displaystyle\sum_{k=1}^n \sum_{j=1}^k1. 3^k \\
&=\displaystyle\sum_{j=1}^n \sum_{k=j}^n 3^k
\end{align}
\)
Après interversion des sommes.
Enfin, on reconnaît la somme des termes d’une suite géométrique de raison \(3 \ne 1 \) et on peut terminer le calcul sans problème.
Tu veux apprendre comment appréhender et intérioriser tous ces astuces ? Alors consulte : Le carnet d’astuces en maths : une bonne idée ?
N’hésite pas à consulter toutes nos autres ressources mathématiques !











