Les bases à maîtriser pour réussir les fonctions en Scilab

Le Scilab est souvent négligé par les candidats aux épreuves de mathématiques. Pourtant, il prend de plus en plus d’ampleur. Tu as donc tout intérêt à travailler cette partie du programme pour te démarquer et gagner de précieux points ! Mais pour cela, encore faut-il maîtriser ce langage informatique. Pour beaucoup, le Scilab semble trop compliqué. Si tu as cliqué sur ce lien c’est que tu ne veux pas que ça soit ton cas aux concours ! On va donc reprendre ensemble les fondamentaux des fonctions en Scilab !

1. Définir une fonction

Dans la majorité des programmes Scilab que tu rencontreras aux concours, ceux-ci contiendront une fonction et il te sera demandé d’en écrire une. Il est donc indispensable de comprendre ces fonctions mais aussi de savoir les écrire !

Définir une fonction f qui prend x en argument et qui renvoie une valeur y se fait comme ça :

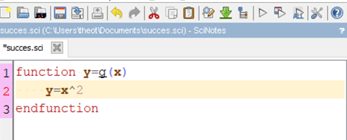
function y=f(x)

expression de y en fonction de x

endfunction

Exemple : (Ici g est donc la fonction carrée)

Remarque : Il est important de noter l’alinéa à la 2^ème ligne du code : celui-ci DOIT être présent sur votre copie ! Sinon vous risquez de perdre des points et cela montre à votre correcteur que vous n’êtes pas rigoureux ! Cela vaut aussi pour le « endfunction » à la fin du code son absence empêche le code de fonctionner et donc il est indispensable sur votre copie !

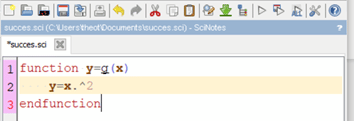
On peut noter que x et y peuvent être des tableaux (autrement dit des matrices) mais quelques modifications doivent alors être apportées dans votre code ! En reprenant l’exemple suivant on a notamment :

2. Les fonctions usuelles

Il faut par ailleurs savoir que certaines fonctions classiques sont déjà paramétrées dans Scilab. Voici notamment celles qui te seront très souvent utiles dans la pratique.

Comme on peut le voir sur le script précédent la commande « // » est très utile, en effet Scilab ignore tout ce qui est écrit après ces doubles slashs ce qui permet donc d’ajouter des informations destinées au correcteur. Cette commande permet aussi de ne pas se perdre dans la rédaction d’un programme. Il se peut enfin que l’énoncé utilise cette commande pour te donner des indications sur le fonctionnement du programme ou encore pour expliciter une commande qui n’est pas au programme.

3. Les paramètres d’une fonction

Cette partie est un peu plus générale et n’est pas directement à propos des fonctions mais c’est très lié !

A. Les valeurs connues par Scilab

Tout d’abord il faut se souvenir que certaines valeurs usuelles sont stockées dans Scilab mais il faut faire attention à ne pas se tromper sur leur appel quand on les utilise sinon ça énerve le correcteur et tu perds des points (oui ça part très vite les points en maths…)

%i = i

%e = e = exp(1)

%pi = π

Le nombre complexe z=a+ib s’écrit donc en Scilab z=a+%i*b .

Il existe d’ailleurs des fonctions permettant de trouver le module d’un complexe z ou bien d’en isoler la partie réelle ou imaginaire :

abs(z) = donne le module de z .

real(z) = donne la partie réelle de z .

imag(z) = donne la partie imaginaire de z .

B. Faire rapidement des tableaux

Deuxième point important qui concerne cette fois les tableaux (ou les matrices). Il existe dans Scilab deux instructions permettant de créer des tableaux particuliers rapidement. Ces instructions ont chacune une utilité précise et ne doivent pas être confondues !

On a d’un côté l’instruction a : h : b  qui renvoie un tableau contenant des valeurs réparties régulièrement dans l’intervalle [a;b] avec un pas de h.

et de l’autre l’instruction linspace(a,b,n) qui renvoie un tableau contenant n valeurs réparties uniformément entre a et b.

Par exemple :

On peut déjà voir la différence entre ces deux instructions au niveau des valeurs renvoyées. Plus précisément, l’instruction linspace permet d’avoir une bonne maîtrise sur le nombre de valeurs contenues dans le tableau là où la première instruction permet d’avoir un bon contrôle sur le pas entre chacune des valeurs (autrement dit elle permet de créer plus facilement une suite logique).

4. Tracer des fonctions

Comme on va le voir, c’est l’instruction plot qui lie le dernier paragraphe aux fonctions et qui rend la maitrise des instructions précédentes indispensable. En effet comme on l’a dit, sur Scilab les fonctions peuvent prendre des tableaux comme paramètres d’entrée. L’instruction plot prend en entrée deux tableaux x=(a,b,c,d) et y=(a’,b’,c’,d’). Il trace alors la courbe de la fonction f définie par a’=f(a), b’=f(b), c’=f(c) et d’=f(d).

Par exemple cela donne (si on rentre les valeurs de y sans réelle logique) :

Ou encore, lorsqu’on veut représenter une fonction usuelle (ici la fonction exponentielle)

On peut remarquer dans un premier temps l’utilité de l’instruction linspace qui permet d’accélérer l’entrée des valeurs d’un tableau et qui peut aussi nous permettre de choisir un nombre de valeurs suffisant pour que la représentation de la fonction proposée par l’instruction plot soit proche de la représentation graphique usuelle de la fonction.

Il est important de noter que l’instruction plot prend en argument deux tableaux de même dimension ! Sinon Scilab retournera une erreur.

5. Pour aller plus loin

Ce paragraphe s’adresse aux personnes déjà à l’aise en informatique. Il s’agit d’un détail qui peut parfaire une copie en informatique.

Lorsque l’énoncé laisse le choix à l’étudiant il est préférable de passer par une fonction plutôt qu’un algorithme basé sur des « input » et des « disp ».

En effet on considère que la seconde approche est plus ancienne et on l’utilisait surtout dans les années 1970-2000.

Exemple :

Les deux algorithmes suivants font la même chose : ils comptent le nombre de succès lors de x répétitions d’une loi de Bernoulli (indépendantes) de paramètres ½.

Autrement dit ils simulent une variable binomiale de paramètres (x,1/2). Cependant le 1^er algorithme est à privilégier par rapport au second si tu maîtrises les deux. Il est évident que tu ne vas pas perdre des points si tu ne suis pas ce conseil mais il peut valoriser ta copie.

6. Conclusion

Comme tu l’as remarqué, il existe de nombreuses subtilités dans la rédaction des fonctions sur Scilab (ne pas mettre des virgules au lieu de points-virgules, ne pas mettre des crochets à la place de parenthèses, bien marquer l’alinéa sur une copie etc…).

C’est cette rigueur qui peut nuire à ta note quand bien même tu aurais rédigé un script correct. C’est pourquoi je te conseille de t’entraîner à rédiger le Scilab aussi bien sur ton ordinateur (pour qu’il fasse apparaître les éventuelles erreurs) mais aussi à la main afin de prendre des réflexes le plus tôt possible.

En effet, sur ordinateur certaines lignes de script se remplissent automatiquement (les alinéas ou la ligne “endfunction” par exemple). Ce remplissage automatique t’empêche de prendre le réflexe de remplir cette commande sur ta copie par exemple.

Enfin, la maîtrise du Scilab va devenir indispensable pour réussir ses concours : on a déjà pu remarquer le fait que le Scilab était de plus en plus présent et de plus en plus complexe et cela peu importe le type de l’épreuve. Pour les aborder sereinement, tu peux aussi lire cet article !