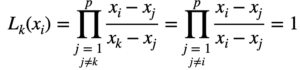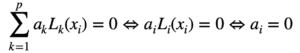Face à la place prépondérante qu’ont les mathématiques en prépa, on te propose aujourd’hui d’étudier des classiques de concours de manière ludique afin que tu puisses les maîtriser le jour J tout en retenant des clefs méthodologiques.
Aujourd’hui, on se penche vers la partie algèbre du programme, en particulier sur ces (jolis) polynômes de Lagrange. Pour ce faire, je te propose d’étudier le sujet EDHEC S 2019 (Tu peux retrouver l’exercice 1 partie 2 ici).
À vos marques… prêts… mathématisons !
Quelques propriétés essentielles
4) a)
Dans le cas i=k on a:
Dans le cas i≠k on a :
En effet, la méthode réside dans le terme j=i que l’on sépare du produit. ainsi cela nous donne bien le résultat précédent.
Ces deux résultats sont fondamentaux et se doivent d’être connu par coeur!
Le principe d’interpolation
4) b) Il s’agit de montrer que (Lk)1≤k≤p est une base de Rp-1[X]
Or, le cardinal de la famille est égal à la dimension de Rp-1[X]: à savoir p. Il reste, alors, à montrer que la famille (Lk)1≤k≤p est une famille libre.
Soit (ak)1≤k≤p p réels : en reprenant la formule précédente et en l’évaluant en xi:
or, avec la 4)a) on sait que lorsque i=k : Li(xi)=1 sinon c’est égal à 0. Il ne reste que le terme en k=i qui est égal à 1 (les autres étant nul).
Donc, (Lk)1≤k≤p est une base de Rp-1[X]
4) c) (Lk)1≤k≤p est une base de Rp-1[X] donc on peut écrire tout polynôme P dans cette base en une unique décomposition: (en soi c’est une application du cours de la définition d’une base !)
Ici on remplace les (ak)1≤k≤p par P(λk) et on a bien le résultat demandé.
4) d) Ici, il suffit juste de prendre la relation de la 4) c) et de remplacer P par le polynôme constant égal à 1.
Conclusion
En résumé, ce petit extrait d’exercice tiré d’une annale EDHEC, montre bien les propriétés fondamentales des polynômes de Lagrange qui vous seront utiles pour le jour J. Cet objet d’étude tombe très fréquemment aux concours et sa maîtrise est plus que conseillée.
La plus grande difficulté réside en les indices muets et non muets qu’il ne faut pas confondre (en témoignent les premiers résultats).
On se retrouve bientôt pour un nouvel objet d’étude!