Tu en as sûrement déjà entendu parler, et pour cause, la théorie des jeux est mobilisable dans d’innombrables domaines d’application : jeux de société (échecs, dames, go), jeux de cartes (poker, bridge), théorie des enchères, science politique, analyse du comportement animal, stratégies militaires et économiques, partage des ressources (marchandage), conditions de travail que devraient imposer une entreprise à ses salariés, dumping fiscal, surexploitation des ressources environnementales (tragédie des communs), coopération internationale, intérêt ou non pour une entreprise d’entrer sur un marché, gestion optimale des relations avec le voisinage et j’en passe !
Si cet article n’a pas vocation à introduire la théorie des jeux – le très bon article de Viktor Gradoux le faisant déjà – il a au contraire pour but d’approfondir certains concepts déjà introduits, d’en expliquer de nouveaux, et d’en présenter quelques applications en économie de la concurrence imparfaite.
L’article est long et technique, mais si tu est motivé(e) et/ou intéressé(e), c’est la garantie de te démarquer en dissertation ou à l’oral en ESH et de marquer des points chez le correcteur/la correctrice ou l’examinateur/l’examinatrice !
Bref historique et rappel de quelques propriétés
L’histoire de la théorie des jeux
Avant de nous lancer, rappelons ce qu’est cette fameuse théorie des jeux. Créée dans les années 1920 par les mathématiciens Borel (1921) et Von Neumann (1928), elle peut être définie simplement comme étant la théorie mathématique des comportements stratégiques. Plus précisément, elle permet d’analyser de manière formelle le comportement d’agents rationnels (les joueurs), calculateurs et maximisateurs, lors d’interactions stratégiques (les jeux) où chacun cherche à atteindre la situation qui est la plus avantageuse pour lui, en fonction de ses préférences. Autrement dit, chaque joueur cherche à maximiser son utilité (d’où l’expression d’agent “maximisateur”).
L’ouvrage fondateur de l’application de la théorie des jeux à l’économie date de 1944 et s’intitule Theory of Games and Economic Behavior. Ouvrage qu’on doit au même Von Neumann et à l’économiste Morgenstern. Le pilier de la théorie des jeux moderne est quant à lui apporté par John Nash en 1950 avec le concept d’équilibre de Nash. Concept qui lui vaudra d’ailleurs le “prix Nobel” d’économie en 1994. En effet, à partir des années 1970, la théorie des jeux est devenue un des indispensables de la boîte à outils de l’économiste, offrant ainsi une visibilité croissante à l’apport théorique de Nash.

Propriétés fondamentales de l’équilibre de Nash
Optimalité de l’équilibre
Enfin, rappelons quelques éléments et propriétés essentiels à garder en tête à propos de l’équilibre de Nash. Premièrement, un équilibre de Nash n’est pas forcément un optimum de Pareto, et peut donc être sous-optimal. Le dilemme du prisonnier montre justement que la situation collectivement souhaitable (l’optimum de Pareto, ici : Ne dénonce pas/Ne dénonce pas) n’est pas celle à laquelle vont aboutir les décisions rationnelles individuelles des agents. On parle aussi parfois de situation anti-smithienne pour décrire cette inadéquation entre l’équilibre effectif (de Nash) et l’équilibre optimal. Équilibre optimal – toujours au sens de Pareto – qui est pourtant justement censé découler des décisions égoïstes des individus dans la (trop ?) célèbre théorie de la main invisible d’Adam Smith.
Existence et unicité de l’équilibre
Par ailleurs, il n’y a pas de garantie qu’il existe un équilibre de Nash dans chaque jeu (dans le cadre de stratégies pures en tout cas), et lorsqu’il existe, il n’y a pas forcément unicité de celui-ci. Dans ce cas, il peut être difficile de choisir vers quel équilibre va tendre le jeu. Si deux équilibres de Nash sont dits “équivalents” s’ils donnent la même utilité à tous les joueurs, l’équilibre vers lequel le jeu va tendre ne sera pas forcément le plus optimal. En effet, dans certains jeux, un équilibre peut paraître plus immédiat et évident que les autres aux différents joueurs en raison de conventions sociales. Pour la culture, un équilibre de Nash résultant de conventions sociales est appelé “point focal”.
Maintenant, voyons à quel point la théorie des jeux s’applique pertinemment à l’économie et plus particulièrement à la concurrence imparfaite et aux structures oligopolistiques !
Les multiples applications de la théorie des jeux aux marchés oligopolistiques
Les marchés oligopolistiques (10-15 producteurs maximum) sont un excellent champ d’application à la théorie des jeux. En effet, les marchés en oligopole sont propices aux interactions stratégiques. Les décisions de production de chaque entreprise ont une influence sur l’équilibre de marché et les entreprises doivent constamment anticiper les plans et les réactions de leurs concurrents. On y observe donc des comportements de type stratégique, i.e. qui déterminent des plans d’action contingents à la réalisation de différentes hypothèses.
On peut, de plus, considérer que l’équilibre d’un marché en oligopole est en réalité un équilibre de Nash, qui va dès lors servir à le formaliser. De fait, comme chaque entreprise prend en compte les actions de ses concurrents et suppose que ses concurrents font de même, l’équilibre en oligopole correspond à une situation où les firmes ont fait les meilleurs choix possibles compte tenu des choix des autres entreprises, et où elles n’ont aucun intérêt à modifier ces choix. On peut donc assimiler l’équilibre de l’oligopole à un équilibre de Nash.
Le modèle précurseur de Cournot (1838)

On considère parfois que le mathématicien français Antoine-Augustin Cournot était un précurseur de la théorie des jeux puisque son fameux modèle de duopole (Recherches sur les principes mathématiques de la théorie des richesses, 1838), forme la plus simple d’oligopole, incorporait une analyse stratégique proche de la théorie des jeux moderne. On peut ainsi considérer que le modèle représente un jeu simultané (autre nom pour jeu statique, par opposition à un jeu dynamique, qu’on peut aussi appeler jeu séquentiel), non coopératif, et à information complète (la structure du jeu, et notamment les courbes de demande sont connues des deux producteurs). Les deux entreprises produisent un même bien et se font donc concurrence sur les quantités.
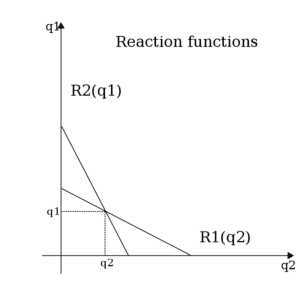
Par ailleurs, chaque firme considère, au moment de choisir les quantités qu’elle va produire, que la quantité produite par sa concurrente est fixée. Le choix optimal de chaque entreprise dépend donc du choix estimé de l’autre, ce qui met bien en évidence un cadre d’interactions stratégiques. Voici ce que donne le modèle, une fois modélisé graphiquement :
On retrouve en abscisses la quantité q2 produite par l’entreprise 2 et en ordonnées la quantité q1 produite par l’entreprise 1. La figure met en évidence ce qu’on appelle les “courbes de réaction” des entreprises. La production de l’entreprise 1, par exemple, est modélisée par la fonction R1 qui prend en argument la variable q2. Quantité q2 qui correspond à l’estimation que fait l’entreprise 1 de la quantité que l’entreprise 2 va produire. Ainsi, l’entreprise 1 va construire un ensemble de meilleures réactions aux décisions potentielles de production de l’autre entreprise pour maximiser son profit.
L’équilibre de Cournot-Nash
L’équilibre, dit de Cournot, se situe lui à l’intersection des courbes de réaction. On le qualifie justement aussi d’équilibre de Cournot-Nash puisque la décision de chaque entreprise est optimale compte tenu de la décision de l’autre entreprise. En effet, à l’équilibre, la quantité produite par l’entreprise 1 est la meilleure réponse à la quantité produite par l’entreprise 2 et la quantité produite par l’entreprise 2 est la meilleure réponse à la quantité produite par l’entreprise 1. Dès lors, chaque firme a correctement anticipé le niveau de production de sa concurrente et a ainsi maximisé son profit.
Les limites du modèle résident dans l’absence d’analyse du processus d’ajustement jusqu’à l’équilibre. Cet ajustement pourrait être formulé selon une logique d’essai-erreur (dans un modèle type cobweb) mais cela irait en contradiction avec l’hypothèse selon laquelle les quantités produites par la firme concurrente sont considérées comme fixées lors de la prise de décision de l’autre entreprise. Le modèle deviendrait alors assimilable à un jeu séquentiel et non plus simultané. Le duopole de Cournot trouve cependant des applications empiriques valides dans les secteurs où les entreprises prennent des décisions de production irréversibles à cause de coûts irrécupérables importants (sunk costs).
Le modèle alternatif de Bertrand (1883)

Un modèle alternatif à celui de Cournot pour analyser les structures oligopolistiques et la concurrence imparfaite, est celui dit de Bertrand, mathématicien français qui avait établi les bases du modèle fin XIXe. Alternatif, car le modèle s’intéresse lui aussi aux duopoles (plus simples à modéliser), mais en faisant l’hypothèse que les entreprises se font concurrence en prix et non plus en quantité. On considère toujours que les biens sont homogènes (identiques) mais aussi que les entreprises n’ont pas de contrainte de capacité : elles peuvent produire autant qu’elles le souhaitent et potentiellement répondre à l’entièreté de la demande sur le marché. Enfin, on fait l’hypothèse que le coût marginal Cm de production du bien est le même pour les deux entreprises. Celles-ci proposent respectivement un prix P1 et P2 et si, par exemple, P1 < P2, alors l’entreprise 1 rafle toute la demande du marché. Si les prix sont identiques, elles se partagent le marché.
L’équilibre de Nash est donc forcément un équilibre où P1 = P2 puisque les entreprises ont toujours intérêt à proposer un prix inférieur à celui de la concurrence, pour s’accaparer toute la demande de marché, tant que le prix est supérieur ou égal à Cm (le profit reste alors positif).
Le “paradoxe de Bertrand”
De fil en aiguille, ou plutôt, de centime en centime, le prix à l’équilibre du duopole de Bertrand, qui est également un équilibre de Nash, finit par être égal à Cm. On obtient alors P1 = P2 = Cm, et donc une tarification similaire à celle observable en concurrence pure et parfaite (CPP). Les deux entreprises font alors un profit nul – résultat bien différent de celui auquel aboutit le duopole de Cournot où les deux entreprises ont un profit strictement positif, plus faible qu’en cas d’entente mais toujours sous-optimal socialement par rapport à la CPP – ce qu’on qualifie de “paradoxe de Bertrand”. En effet, le modèle semble montrer que deux entreprises sur un marché suffiraient à restaurer l’équilibre concurrentiel.
Les limites du modèle de Bertrand résident dans le fait qu’empiriquement, la concurrence se fait plutôt sur les quantités quand les biens sont homogènes, et que dans une situation d’oligopole, la concurrence par les prix est en réalité souvent combinée à une stratégie de différenciation (comme sur le marché automobile). Par ailleurs, le modèle ne donne pas d’information sur la répartition de la demande lorsque les deux entreprises pratiquent un prix identique. Le duopole de Bertrand a cela dit le mérite de mettre en évidence, à la fois, l’intérêt pour les oligopoleurs de s’entendre sur les prix, et en même temps, l’instabilité potentielle que pourrait revêtir une telle entente.
Application du dilemme du prisonnier au choix entre concurrence et collusion dans un oligopole
Et d’ailleurs, le plus célèbre des jeux peut ici apporter une clé d’analyse complémentaire au modèle de Bertrand pour comprendre le choix, ou le non choix, pour des entreprises en situation d’oligopole, de s’entendre. La situation préférable collectivement pour deux entreprises en duopole (pour simplifier) serait de s’entendre pour faire payer un prix plus élevé : 6€ par exemple rapportant à chaque entreprise 16€ de profit. Cela dit, en anticipant le fait que l’autre pourrait me tromper et baisser son prix à 4€ pendant que je suis resté à 6€ (faisant passer son profit à 20€, et le mien à 4€), je décide alors de faire payer 4€ et de faire concurrence à l’autre duopoleur plutôt que de m’entendre avec lui.
Le raisonnement étant symétrique pour l’autre firme, l’équilibre de Nash est donc : Faire payer 4€/Faire payer 4€ ce qui rapporte à chaque entreprise 12€ de profit. La collusion serait donc la situation préférable collectivement mais celle-ci serait instable dans le cadre d’un jeu non coopératif. Le dilemme du prisonnier explique donc le fait que la stratégie d’entente est strictement dominée par la stratégie de se faire concurrence : peu importe le choix de l’autre, mes gains sont supérieurs si je pratique un prix de 4€.
Limites des prédictions théoriques de l’équilibre de Nash
Ce résultat de la théorie des jeux appliqué aux ententes était proposé par Stigler en 1964. Pour lui, les cartels sont nécessairement instables puisque le dilemme du prisonnier met en évidence les intérêts rationnels à la triche et au non respect de l’entente. Selon lui, les cartels ont une durée de vie maximale strictement inférieure à un an. Cela dit, empiriquement, la durée de vie moyenne des cartels en Europe est de 7 ans (Combe & Monnier, 2012), ce qui remet en cause le résultat du dilemme du prisonnier, et, plus généralement, les prédictions théoriques de l’équilibre de Nash.
Motivations sociales…
On peut expliquer ces limites par le fait que le gain monétaire ne reflète pas la totalité des préférences des agents, qui peuvent aussi avoir des motivations sociales. Le sentiment de culpabilité, par exemple, peut diminuer le gain d’utilité qu’apporterait la rupture mesquine d’une entente pour gagner plus d’argent au détriment de l’entreprise partenaire. Or, en théorie, pour conclure à l’existence d’un équilibre de Nash, il faudrait d’abord être sûr que les gains du jeu permettent de révéler entièrement les préférences des agents, ce que ne font donc pas forcément des gains purement monétaires.
… et rationalité limitée
Une autre explication réside dans la potentielle rationalité limitée des agents (Hebert Simon, 1943). Ainsi, Nicolas Eber explique en 2015 dans Problèmes Économiques que, même dans des expérimentations où l’on essaye au maximum de neutraliser les motivations sociales, les résultats restent éloignés de l’équilibre de Nash.
Prenons un jeu à 2 partenaires où chacun doit choisir un nombre entre 0 et 100. Le vainqueur du jeu est celui dont le nombre choisi sera le plus proche de la moitié de la moyenne des deux nombres donnés. Le vainqueur reçoit 10€, et en cas d’égalité chacun obtient 5€. En théorie, le seul équilibre de Nash correspond au choix par les deux joueurs du nombre 0. En effet, 0 assure systématiquement, soit la victoire, soit l’égalité (soit X le nombre choisi par l’autre joueur, 0 est toujours plus proche de 1/2 * X/2 = X/4 que X) : on dit alors que choisir 0 est une stratégie faiblement dominante.
Pourtant, lorsqu’on expérimente empiriquement ce jeu, avec de réels enjeux monétaires pour les joueurs, on obtient que moins de 10% des sujets étudiants choisissent 0 et moins de 40% des économistes professionnels. Or, il semble difficile de voir ici une autre motivation pour le joueur que de maximiser son gain monétaire. C’est donc l’hypothèse de la rationalité limitée qui semble expliquer le décalage entre le résultat empirique et le résultat théorique.
Répéter pour mieux coopérer
Une autre raison peut enfin expliquer le décalage entre le résultat de Stigler et l’empirie : une logique de coopération peut se créer dans des jeux répétés, que le dilemme du prisonnier statique ne peut comprendre. C’est donc l’occasion de passer le dilemme du prisonnier en forme extensive et d’analyser l’apport théorique de sa version dynamique. On qualifie cette version de dilemme itéré du prisonnier.
Le dilemme itéré du prisonnier
Dans le dilemme itéré du prisonnier (DIP), le jeu initial du dilemme du prisonnier se répète dans le temps (imaginons que les 2 prisonniers ont commis plusieurs crimes) : les joueurs jouent toujours simultanément, au même jeu, mais se rencontrent plusieurs fois. On considère également qu’à chaque itération, les joueurs ont connaissance des coups précédents (jeu à information parfaite) et qu’ils ne savent pas quand les itérations s’arrêteront (la liste des crimes est trop longue pour qu’ils s’en souviennent…). On parle alors de jeu à horizon infini. Enfin, on considère que le gain d’un joueur correspond à la somme des gains obtenus après chaque sous-jeu.
Si le DIP peut par exemple être utilisé pour savoir si un pays devrait imposer des droits de douane sur les produits qu’il importe d’un autre pays, nous l’utiliserons ici pour résoudre le dilemme posé précédemment entre collusion et concurrence dans un oligopole. En effet, dans la réalité, on observe une répétition des interactions stratégiques entre oligopoleurs, et donc, des jeux.
La stratégie donnant-donnant
Robert Axelrod, un théoricien des jeux, a étudié dans son ouvrage The Evolution of Cooperation (1984) différentes stratégies qu’il est possible de mettre en place dans le DIP, en testant leur efficacité (en termes de gains cumulés), informatiquement, lors de tournois. Il montre que chaque stratégie est bonne face à certaines et mauvaises face à d’autres. La stratégie méchante par exemple (toujours dénoncer) permettrait au joueur qui la joue de maximiser son gain face à un joueur qui utiliserait la stratégie gentille (ne jamais dénoncer). Joueur qui, lui, finirait avec un gain minimal. Mais ce résultat ne suffit pas à déclarer que la stratégie méchante est la plus efficace puisqu’une stratégie méchante contre une autre stratégie méchante obtiendrait, par exemple, un gain inférieur à celui d’une stratégie gentille contre une autre stratégie gentille.
Finalement, à l’issue d’un tournoi opposant 2 à 2 des stratégies proposées par des théoriciens des jeux à Axelrod, avec 200 itérations du dilemme du prisonnier à chaque face-à-face, la stratégie donnant-donnant, ou “oeil pour oeil”, est celle qui s’est avéré avoir obtenu le gain cumulé le plus élevé parmi toutes les stratégies. Un deuxième tournoi a par la suite confirmé ce résultat. La meilleure stratégie à adopter dans le DIP semble donc être de coopérer au premier tour, puis de coopérer si l’autre joueur a également coopéré lors du dernier sous-jeu, ou alors de le trahir s’il nous a trahi lors du tour précédent. Fait intéressant : donnant-donnant ne gagne contre aucune autre stratégie, ce qui ne l’empêche pas, in fine, d’être la meilleure !
Appliquée au dilemme entre collusion et concurrence, la stratégie “oeil pour oeil” préconise donc de commencer la partie avec un prix élevé, dans une logique coopérative, puis de baisser les prix au sous-jeu suivant si l’autre joueur les a baissés dès le premier tour. S’il les augmente à ce sous-jeu-là, alors la stratégie donnant-donnant conseille de les augmenter également au prochain sous-jeu.
Jeu à horizon infini ou fini ?
Dans ce cadre, la coopération apparaît comme la solution rationnelle puisque, comme on sait que l’autre joueur joue également donnant-donnant, étant donné que c’est la meilleure stratégie, la moindre baisse des prix d’un côté ou de l’autre entraînera une guerre des prix qui occasionnera davantage de pertes que de gains. Cela dit, on peut se demander si, dans la pratique, il est réellement possible de considérer qu’un jeu séquentiel puisse être à horizon infini.
En effet, dans un jeu à horizon fini, les prédictions théoriques ne sont pas les mêmes puisque chaque entreprise, toujours dans une stratégie donnant-donnant, aurait intérêt à baisser les prix au dernier jeu. Cependant, comme chaque firme sait que l’autre compte faire cela, alors elles vont prévoir de baisser les prix à l’avant dernier-jeu, etc. On assiste alors à un “détricotage” du jeu qui fait tomber la coopération à l’eau.
Cette résolution rationnelle du jeu par la méthode de l’induction à rebours, aussi appelée récurrence à rebours (backward induction) – qui consiste à faire le choix optimal à la dernière période puis à remonter vers le présent en déterminant pour chaque sous-jeu les choix optimaux, compte tenu des choix déjà faits – conduit à un équilibre de Nash “parfait” (Selten, 1965). Cela signifie que chaque sous-jeu possède un équilibre de Nash, mais qu’en plus ces équilibres sont crédibles séquentiellement. Le jeu va donc nécessairement converger vers cet équilibre de Nash parfait, qui, en l’occurrence, annule totalement les perspectives de collusion entre oligopoleurs.
Jeu à horizon fini incertain
Cela dit, si la réalité semble a priori plus proche d’un jeu à horizon fini (la durée de vie d’un humain n’est pas infinie), il est possible d’affiner en considérant que nos oligopoleurs jouent en fait un jeu à horizon fini incertain (puisqu’ils ne connaîssent pas la date de la fin du jeu, i.e. de leur mort). La théorie des jeux permet alors tout de même d’expliquer rationnellement la possibilité d’une entente entre firmes dans le cadre d’un dilemme itéré du prisonnier à horizon fini incertain, en se ramenant aux conclusions d’un DIP à horizon infini.
La collusion peut aussi émerger à nouveau si un joueur considère que l’autre a une rationalité limitée : qu’il joue donnant-donnant à l’aveugle, et qu’il n’a donc pas élaboré un raisonnement rigoureux par induction à rebours. Le risque de détricotage du jeu disparaît alors et l’entente peut s’établir, et se stabiliser (ou pas). En effet, la stabilité de la coopération est encore loin d’être garantie.
Pour conclure
Si la possibilité d’une collusion entre entreprises peut dorénavant se comprendre théoriquement, toute une branche de la théorie des jeux doit encore intervenir et prendre le relai pour déterminer l’instabilité potentielle d’une entente : celle des jeux coopératifs. Cette branche, initiée par Von Neumann et Morgenstern, s’intéresse aux situations où les joueurs peuvent communiquer entre eux pour s’accorder et coordonner leurs actions. Vous l’aurez compris, les ressources qu’offrent la théorie des jeux pour l’analyse et la compréhension de la concurrence imparfaite, et des phénomènes économiques de manière plus large, sont donc loin de se tarir.
Critiques et flexibilité de la théorie des jeux
La théorie des jeux n’est cela dit pas exempte de toute critique, considérée comme le parachèvement de la mathématisation de l’économie par nombre d’économistes orthodoxes. L’économiste atterré David Cayla déplore par exemple l’absence de prise en compte de l’influence des institutions sociales et des rapports de domination sur l’action des agents. La théorie des jeux serait dès lors déconnectée de la réalité sociale et politique, mettant sous silence le lien entre les structures économiques et le pouvoir, tout comme le fait le reste de l’économie standard.
Cependant, la force du cadre conceptuel de la théorie des jeux réside dans sa flexibilité, capable d’intégrer de nouveaux paramètres aux modèles comportementaux des joueurs, sans remettre en cause ses fondements théoriques comme le concept d’équilibre de Nash. Le développement moderne de la théorie des jeux comportementale prouve d’ailleurs cette flexibilité puisqu’elle intègre des facteurs psychologiques à l’analyse du comportement des joueurs, sur la base d’observations expérimentales.
Or, comme observé dans l’article, des expérimentations ont déjà mis en évidence la possibilité que des motivations sociales, et non simplement monétaires, animent les joueurs. A charge pour la théorie des jeux de continuer à évoluer conceptuellement pour pouvoir penser ces réalités-là et enrichir davantage l’analyse économique.
Ce qu’il faut retenir de l’article
Il est peut-être temps de faire une synthèse de ce qu’il faut retenir de cet article chargé en informations.
Tout d’abord, la théorie des jeux, c’est la théorie mathématique des comportements stratégiques. Utilisable dans énormément de domaines, on doit son application à l’économie à Von Neumann et à Morgenstern (1944), et sa prise d’ampleur à John Nash, prix “Nobel” d’économie et créateur de l’équilibre de Nash (1950). Cet équilibre correspond à une situation dans laquelle chaque joueur a pris la meilleure décision compte tenu des décisions qu’il a anticipé que les autres prendraient. Cette situation peut ne pas être optimale au sens de Pareto, et il n’est pas garanti que cet équilibre soit unique, ni même qu’il existe un équilibre de Nash pour chaque jeu.
Ensuite, les structures oligopolistiques sont un excellent champ d’application pour la théorie des jeux. On peut d’ailleurs considérer que l’équilibre d’un oligopole est un équilibre de Nash puisque chaque entreprise prend ses décisions en fonction des décisions des autres entreprises. Cournot en avait déjà eu l’intuition en 1838 dans son modèle du duopole où les courbes de réactions des entreprises modélisaient cette idée d’interactions stratégiques entre les firmes. Le modèle de Bertrand de 1883 qui considère que les entreprises se font concurrence en prix et non en quantité comme pour Cournot, faisait lui aussi intervenir des comportements stratégiques qui ont abouti au paradoxe de Bertrand. Celui-ci avance que deux entreprises sur un marché suffisent à rétablir l’équilibre concurrentiel de la CPP.
Par ailleurs, la théorie des jeux, et notamment le dilemme du prisonnier, permet également d’expliquer pourquoi la stratégie d’entente entre entreprises est strictement dominée par celle de se faire concurrence. Ce résultat proposé par Stigler en 1964 est cependant remis en cause empiriquement puisque les cartels ont en Europe une durée de vie moyenne de 7 ans. Cet écart peut s’expliquer par le fait que les gains monétaires ne reflètent pas la totalité des préférences des agents, qui peuvent avoir des motivations sociales, ou par le fait que ceux-ci peuvent tout simplement avoir une rationalité limitée. Une dernière raison peut être le fait que, dans la réalité, les jeux sont répétés, ce qui peut modifier les prédictions théoriques du dilemme du prisonnier et expliquer la possibilité d’une coopération entre entreprises.
L’analyse de sa version dynamique : le dilemme itéré du prisonnier (DIP), permet alors de conclure, grâce à des simulations informatiques, que la coopération est possible théoriquement. En effet, la meilleure stratégie s’avère être la stratégie donnant-donnant (aussi appelée « œil pour œil ») qui consiste à coopérer par défaut mais à rompre la coopération si l’autre joueur le fait avant nous (Axelrod, The Evolution of Cooperation, 1984). Or, dans un jeu à horizon infini, la conséquence de cette stratégie est la coopération entre les joueurs, puisqu’aucune firme jouant donnant-donnant n’a intérêt à rompre la coopération. Et puisque la vie peut être assimilée à un jeu à horizon fini incertain, ce qui équivaut à un jeu à horizon infini, la théorie des jeux peut finalement rendre compte des résultats empiriques qui observent la possibilité d’une collusion entre oligopoleurs.
Voilà ! J’espère que tu es désormais un(e) pro de la théorie des jeux, prêt(e) à briller dans cette riche et dense matière qu’est l’ESH et à impressionner tes futur(e)s correcteurs/correctrices et examinateurs/examinatrices ! Retrouve toutes les autres ressources pour travailler l’ESH sur notre site ici !