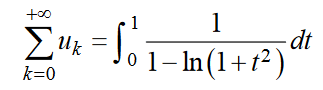Tu peux retrouver le sujet de l’épreuve ici : Sujet de maths EDHEC 2018 ECE
Et l’analyse là : Maths EDHEC 2018 ECE – Analyse du sujet
Les statistiques
3 844 candidats, 10,74 de moyenne (6,35 d’écart-type).
Le rapport
Présentation de l’épreuve
L’épreuve comportait, comme d’habitude, trois exercices et un problème, ce qui permettait de juger les candidats sur une partie conséquente du programme des classes préparatoires.
Le sujet balayait largement le programme en donnant, comme d’habitude, une place importante aux probabilités (deuxième et troisième exercices).
La diversité des thèmes abordés a permis à tous les candidats de s’exprimer et de montrer leurs compétences, ne serait-ce que sur une partie du programme.
Deux exercices et le problème comportaient une ou deux questions d’informatique.
Dans l’ensemble, les correcteurs ont trouvé le sujet un peu long (comme d’habitude), parcourant une bonne partie du programme d’ECE, équilibré, bien adapté au public concerné (de nombreuses questions étaient faisables), et suffisamment discriminant par la présence de questions techniquement difficiles ou abstraites.
Description du sujet
L’exercice 1 proposait l’étude de l’endomorphisme de M2 (ℝ) défini par F ( M ) = AM , où A est une matrice quelconque de M2 (ℝ) . Une première partie s’intéressait au cas où A = (13 62), avec détermination du noyau, de l’image et des sous-espaces propres de F.
Cet exercice a été abordé avec des fortunes diverses, surtout dans les dernières questions, mais c’est globalement le mieux réussi.
L’exercice 2, portait sur la partie probabilités du programme et étudiait le lancer d’une pièce choisie au hasard parmi trois pièces : une pièce numérotée 0, pour laquelle la probabilité d’obtenir “pile” valait 1/2 et celle d’obtenir “face” valait également 1/2, une pièce numérotée 1, donnant “face” à coup sûr et une troisième pièce, numérotée 2, donnant “pile” à coup sûr.
L’objectif était de déterminer les lois de X, Y et X + Y où X désignait le rang du premier “pile” obtenu et Y celui du premier “face”. Un script, s’il était complété correctement, permettait d’obtenir une simulation de X.
Comme d’habitude, la formule des probabilités totales a été copieusement martyrisée par de nombreux candidats et cet exercice a permis de départager de façon tranchée les candidats. Il est le moins bien réussi avec le problème.
L’exercice 3 portant également sur la partie probabilités du programme, avait pour objectif principal d’estimer, ponctuellement et par intervalle de confiance, le paramètre A strictement positif de la loi suivie par une variable aléatoire X dont une densité était donnée par :
Avant ceci, on donnait une simulation de la variable X, puis on calculait espérance et variance de X.
L’inégalité de Bienaymé-Tchebychev est mal maîtrisée par de nombreux candidats.
Le problème, portant sur le programme d’analyse proposait, dans la première partie, l’étude d’une intégrale fonction de sa borne supérieure, à savoir la fonction F définie sur ℝ par :
On cherchait plus précisément des équivalents de F ( X) aux voisinages de −∞ , 0 et +∞ .
La deuxième partie avait pour objectif d’étudier une suite associée à cette fonction, à savoir la suite (UN ) définie par :
On souhaitait notamment montrer que la série de terme général UN convergeait et ensuite, établir le résultat suivant :
Statistiques
Pour l’ensemble des 3844 candidats ayant composé, la moyenne obtenue à cette épreuve est égale à10,738 sur 20 (presque identique à celle de l’année dernière) et l’écart type vaut 6,354 (supérieur de 0,3 point à celui de l’année dernière, et toujours très important).
38,6% des candidats, contre 37,2% l’année dernière, ont une note strictement inférieure à 8 (dont 17,5%, ont une note inférieure à 4 contre 16,4% l’année dernière).
18,8% des candidats ont une note comprise entre 8 et 12 (pourcentage un peu inférieur à celui de 2017 qui était égal à 19,7%).
27,3% des candidats ont une note supérieure ou égale à 16 (pourcentage supérieur à celui de 2017 qui était égal à 24,3%).
Conclusion
Comme l’an dernier, le niveau est très hétérogène et l’impression générale ressentie à la lecture des copies amène à penser que les questions les plus subtiles, qui demandent une compréhension fine de la théorie, quel que soit le domaine concerné, échappent à presque tous les candidats. Les meilleurs ont acquis des techniques et des réflexes mais ne comprennent pas forcément ce qu’ils font.
Les copies sont, dans l’ensemble, bien présentées malgré la présence d’un nombre assez élevé de candidats qui ne respectent pas la numérotation des questions, voire même l’oublient, écrivent mal (ce sont souvent les mêmes) et rendent la tâche du correcteur pénible : qu’ils sachent qu’ils n’ont rien à gagner à pratiquer de la sorte, bien au contraire.
Pour terminer ce paragraphe, il reste toujours un noyau de candidats qui ne peuvent s’empêcher de faire du remplissage au lieu d’argumenter face aux questions dont le résultat est donné : ceci est vécu comme une fraude (mot utilisé par plusieurs correcteurs).
Les candidats ne doivent pas oublier qu’une épreuve de concours valide deux années d’étude : il faut donc garder en tête les connaissances de première année.
L’investissement en informatique, à peu près stable par rapport à l’année dernière, a permis à de nombreux candidats de glaner des points sans y passer énormément de temps, certains correcteurs trouvant d’ailleurs que le barème était trop généreux de ce point de vue.
Précisons pour les futurs candidats qu’ils ne sont pas obligés de recopier les énoncés des questions avant de les traiter et qu’ils ne sont pas, non plus, obligés de recopier tout un programme d’informatique si la question posée était seulement de compléter quelques instructions manquantes.
Rappelons, comme d’habitude, que l’honnêteté, la simplicité, la précision et la rigueur sont des vertus attendues par tous les correcteurs sans exception, et qu’une bonne réponse est toujours une réponse construite rigoureusement.