Maîtriser le modèle de Solow de la croissance économique est primordial pour deux raisons. Premièrement, il s’agit de la vision néoclassique traduite dans un modèle pour expliquer la croissance. Deuxièmement, si vous avez un sujet qui porte sur l’épargne, sur les innovations et/ou le progrès technique, la démographie, le développement (et le rattrapage des PED) ou encore l’état stationnaire, ce modèle est à mobiliser !
Modèle de Solow : les hypothèses fondamentales de son modèle
Solow : économiste de la synthèse
Solow est un économiste de la synthèse : il est néoclassique lorsqu’il s’agit d’analyser le long terme, et keynésien à court terme. Ainsi, à long terme, le marché s’autorégule, et à court terme, le marché n’est pas efficient : il existe des équilibres de sous-emplois.
Dans le modèle de Solow, la croissance est un phénomène de long terme, le court terme étant marqué par le cycle économique. [Gardez bien cette distinction en tête : lorsque l’on vous demande d’analyser les cycles économiques, ce ne sont pas les phénomènes de croissance que l’on vous demande d’analyser !] Pour analyser la croissance, nous nous plaçons donc dans un cadre théorique néoclassique : ainsi, les hypothèses suivantes seront celles des néoclassique !
Le respect des hypothèses néoclassiques
Pour les néoclassiques, la croissance économique est un phénomène quantitatif, deux facteurs de production permettent de produire : le travail (L) et le capital (K). Si vous voulez augmenter la quantité produite (que l’on va confondre ici avec Y, le revenu national), il suffit d’augmenter la quantité de travail et/ou de capital. Ainsi, Q = Y = F(K,L) donc augmenter Q revient à augmenter K et/ou augmenter L.
Les facteurs travail et capital sont substituables dans le modèle de Solow : cela signifie que pour produire Q, je peux choisir de remplacer du travail par du capital et vice-versa : j’effectue ce choix en fonction du prix du L et du prix du K. On utilise un coefficient alpha pour indiquer la proportion de K et la proportion de L que l’on va utiliser pour produire.
D’autre part, Q (la quantité produite) est égal à Y (le revenu national), ce qui nous permet d’écrire : Q = Y = K^ α*L^(1-α) et en général α vaut ⅔ en moyenne. Ces facteurs ont une productivité marginale décroissante et cette fonction de production (Y) est à rendement d’échelle constant.
La croissance permise par l’équilibre sur le marché des B&S, qui suppose l’égalité I = S
1) Une conception NC et keynésienne de l’épargne dans le modèle de Solow
Le taux d’intérêt permet d’arbitrer entre épargne & investissement (NC)
L’équilibre sur le marché des B&S en économie fermée s’effectue lorsque l’investissement égalise l’épargne, c’est-à-dire lorsque S = I.
Dans une analyse néoclassique, l’épargne est fonction croissante du taux d’intérêt, que l’on note “i” et l’investissement une fonction décroissante de i. Les individus effectuent un choix intertemporel à partir du taux d’intérêt, qui détermine s’ils épargnent ou s’ils investissent.
L’épargne est un profit pour les épargnants : les individus sont prêts à renoncer à 1 € aujourd’hui si demain il leur rapporte 1+i€ ; a contrario, les individus préféreront investir (c’est-à-dire dépenser aujourd’hui cet argent) si l’intérêt est faible : pour les investisseurs, le taux d’intérêt est un coût, il s’agit du coût d’emprunt, plus ce coût est faible et plus ils investiront. Ainsi, le taux d’intérêt permet d’équilibrer l’épargne et l’investissement, et permet donc S = I.
Dans une perspective néoclassique, il y a équilibre sur le marché des biens et des services lorsque le rapport des productivités marginales des facteurs de production est égal au rapport de leur prix !
Or, le taux d’intérêt est le prix du capital (ce même taux d’intérêt qui égalise I & S) ! Le salaire est le prix du travail.
w / i = Prix du L / Prix du K = PmL / PmK
Vous le voyez le lien avec Y ? Le bon taux d’intérêt, qui égalise I & S, doit également permettre d’obtenir la combinaison efficace de L & de K pour produire.
L’épargne : ce qu’il reste après avoir consommé (Keynes)
Une contradiction émerge : le modèle de Solow affirme également, dans une perspective keynésienne, que l’épargne est un résidu ! Pour Solow, l’épargne est également la partie que l’on n’a pas consommée du revenu : difficile de concilier cette vision de l’épargne, comme résidu, avec la vision néoclassique qui considère l’épargne comme le résultat d’un arbitrage intertemporel (avec le taux d’intérêt).
On notera donc :
I = S = s.Y, avec s = Y/S la propension à épargner.
2) L’équilibre sur le marché des biens & services
L’égalité entre l’offre et la demande, sous condition de I = S
Pour qu’il y ait croissance, il faut qu’il y ait équilibre sur le marché des B&S : il ne peut y avoir d’équilibre sur le marché des B&S sans l’égalité entre l’investissement et l’épargne.
- X = M = 0 (on est en économie fermée) & O = D à condition que I = S
- O = D = C + I avec I = S [d’habitude, vous écrivez que la demande est la demande privée, celle des ménages (C + I) & la demande publique (G) celle de l’Etat, or ici il n’y a pas d’Etat]
La représentation graphique du modèle de Solow
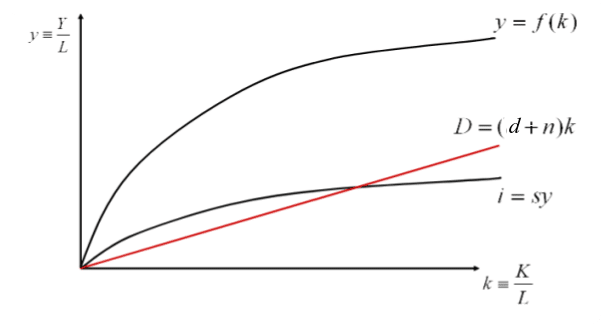
Pour représenter sur un graphique la fonction de la croissance économique, qui je le rappelle dépend de la quantité de facteur travail & capital – et est donc une fonction à deux variables, nous allons la “transformer” en une fonction à une variable. Nous allons uniquement raisonner à partir du travail et diviser chaque membre de l’égalité Y = F(L,K) par L. On obtient une fonction à une variable notée y = f(k).
Nous avons, ainsi, y = Y/L, qui représente la productivité du travail et k = K/L l’intensité capitalistique avec laquelle un travailleur produit (c’est-à-dire la quantité de capital par travailleur).
On a également l’égalité I = S qui est divisée par L, or S = sY. On obtient i = I/ L = S / L = s.[Y/L] et donc i = sy
Pourquoi cette courbe de la croissance a-t-elle cette forme ?
Comme vous le voyez, au début, la croissance augmente très fortement, puis il arrive un moment où elle devient constante. Cela s’explique par la loi des rendements factoriels décroissants (hypothèses du modèle) : la productivité marginale du capital finit par décroître. Au bout d’un moment, à quantité de facteur travail constant, augmenter ma quantité de capital ne permettra plus d’augmenter le produit intérieur brut.
Ainsi la dépréciation du stock de capital entraîne un ralentissement de la croissance économique.
Quels sont les facteurs qui peuvent déprécier le stock de capital et ainsi ralentir la croissance économique ?
- La croissance démographique (notée n) : plus le nombre de travailleurs augmente (L), plus l’intensité capitalistique diminue et k diminue, ce qui diminue la quantité produite.
- La détérioration du capital (noté d) : on appelle cela le déclassement. Le stock de capital a une durée de vie, exemple : une machine à laver fonctionne 3 ans puis est hors d’usage. Ainsi, chaque année le capital se déclasse, c’est-à-dire qu’il perd de sa valeur chaque année jusqu’à finir par ne plus fonctionner.
Notons D la fonction de détérioration du capital : D = f(n,k,d). Représentons cela graphiquement en postulant que chaque année une même proportion du capital se détériore :
Il y a croissance économique à mesure que D < i, c’est-à-dire, tant que l’accumulation de capital couvre suffisamment la détérioration du stock de capital. Plus précisément, tant que l’investissement net (Inet = i – D) est positif, il y a de la croissance économique.
Si l’on investit suffisamment dans une économie pour renouveler le stock de capital, alors la croissance économique se poursuit. Le point de rencontre entre la droite D et la courbe i est le point où se situe l’état stationnaire : moment où l’économie stagne.
Le phénomène de convergence des économies : rattrapage des pays pauvres
On observe également que toutes les économies tendent vers l’état stationnaire : un pays pauvre, avec un faible niveau de K, pourra se développer grâce à une hausse de l’épargne, mais il finira par atteindre le niveau k* là où D = I et là où se situe l’état stationnaire.
Comment définir l’état stationnaire ? C’est un état de l’économie où le capital croît au même rythme que toutes les autres variables, c’est-à-dire à un taux 0.
Comment retarder le moment où l’économie atteint l’état stationnaire ?
- Le progrès technique, qui permettrait d’augmenter la rentabilité du capital, permet de retarder l’état stationnaire. Problème : pour Solow, le progrès technique n’est pas produit par l’économie, il est exogène : c’est une manne céleste qui tombe du ciel…
- La croissance de la croissance démographique (n) : la hausse de n est bénéfique, il permet de diminuer les salaires ( w < i) et d’inciter ainsi les entrepreneurs à investir dans le capital.
- L’augmentation du taux d’épargne (ou du taux d’investissement) permettrait d’avoir Inet > 0 car on pourrait avoir i > D.