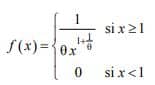Tu peux retrouver le sujet de l’épreuve ici : Sujet de maths EDHEC 2019 ECE
Et l’analyse là : Maths EDHEC 2019 ECE – Analyse du sujet
Les statistiques
3 841 candidats, 10,12 de moyenne (6,18 d’écart-type).
Le rapport
Présentation de l’épreuve
L’épreuve comportait, comme d’habitude, trois exercices et un problème, ce qui permettait de juger les candidats sur une partie conséquente du programme des classes préparatoires.
Le sujet balayait largement le programme en donnant, comme d’habitude, une place importante aux probabilités (deuxième exercice et problème).
La diversité des thèmes abordés a permis à tous les candidats de s’exprimer et de montrer leurs compétences, ne serait-ce que sur une partie du programme.
Des questions d’informatique étaient proposées dans les exercices 2 et 3, ainsi que dans le problème.
Dans l’ensemble, les correcteurs ont trouvé le sujet bien adapté au public concerné, mais comportant, peut-être un peu plus que l’année dernière, quelques questions particulièrement difficiles (fin de l’exercice 1, exercice 2 et partie 1 du problème notamment) où seuls les très bons candidats ont pu tirer leur épingle du jeu en montrant leur capacité à mener un calcul compliqué à son terme ainsi que leur faculté à raisonner sur des situations abstraites.
Description du sujet
L’exercice 1 portant sur la partie algèbre linéaire du programme, étudiait l’inversibilité et la diagonalisabilité de la matrice 
. Ensuite, on trouvait une matrice triangulaire T semblable à A qui permettait alors de caractériser le commutant de A et d’en trouver une famille génératrice.
Cet exercice, dont les trois premières questions étaient assez faciles, a permis, par les questions suivantes, de parfaitement classer les candidats selon leur faculté à abstraire et à raisonner sur des concepts délicats d’algèbre linéaire.
L’exercice 2 portait sur la partie probabilités du programme et étudiait une succession de tirages dans une urne contenant une boule noire non numérotée et n −1 boules blanches dont n − 2 portent le numéro 0 et une porte le numéro 1. Les boules étaient extraites au hasard, une à une, sans remise, jusqu’à l’apparition de la boule noire.
L’objectif était de déterminer la loi de la variable aléatoire X, égale au rang d’apparition de la boule noire, ainsi que la loi de la variable aléatoire Y, qui valait 1 si la boule numérotée 1 avait été piochée lors de l’expérience précédente, et qui valait 0 sinon.
Deux scripts, s’ils étaient complétés correctement, permettait d’obtenir une simulation de X et de Y.
Comme d’habitude, la formule des probabilités totales et celle des probabilités composées ont été copieusement martyrisées par de nombreux candidats et cet exercice a permis de départager de façon tranchée les candidats. Il est, de loin, le moins bien réussi de cette épreuve.
L’exercice 3 portant sur la partie analyse du programme, proposait l’étude de la suite (un ) définie par : 
On cherchait plus précisément un équivalent de (un) au voisinage de +∞ .
Cet exercice a été globalement bien réussi bien qu’un nombre non négligeable de candidats se trompent en développant (1-t²)² et en calculant des primitives de fonctions polynomiales.
Le problème, portant sur la partie probabilités du programme, proposait l’étude d’une variable aléatoire X de densité f définie par :
La partie 2 en proposait la simulation et la partie 3 s’intéressait à l’estimation (ponctuelle, puis par intervalle de confiance) du paramètre θ.
Ce problème a été abordé avec des fortunes diverses, surtout dans les premières questions, où, comme dans l’exercice 3, la recherche de primitives a posé problème à beaucoup de candidats.
Statistiques
Pour l’ensemble des 3841 candidats ayant composé, la moyenne obtenue à cette épreuve est égale à 10,12 sur 20 (inférieure de 0,6 point à celle de l’année dernière) et l’écart type vaut 6,18 (inférieur de 0,17 point à celui de l’année dernière, et toujours très important).
42,8% des candidats, contre seulement 38,6% l’année dernière, ont une note inférieure à 8 (dont 21,4% ont une note inférieure à 4 contre 17,5% l’année dernière).
17,8% des candidats ont une note comprise entre 8 et 12 (pourcentage un peu inférieur à celui de 2018 qui était égal à 18,8%).
22,3% des candidats ont une note supérieure ou égale à 16 (pourcentage inférieur à celui de 2018 qui était égal à 27,3%).
Conclusion
Comme l’an dernier, le niveau est très hétérogène et l’impression générale ressentie à la lecture des copies amène à penser que les questions les plus subtiles, qui demandent une compréhension fine de la théorie, quel que soit le domaine concerné, échappent à presque tous les candidats. Les meilleurs ont acquis des techniques et des réflexes mais ne comprennent pas forcément en profondeur ce qu’ils font.
Les copies sont, dans l’ensemble, bien présentées et bien rédigées mais il reste des candidats qui rendent pratiquement un brouillon, truffent leur copie d’abréviations non officielles, proposent des copies sales et raturées, parfois sans les numéros des questions traitées ou avec des numéros fantaisistes (avec la numérisation des copies, c’est réellement un “jeu dangereux”).
Sur le fond, un nombre non négligeable de candidats restent adeptes des réponses floues et du bluff : il faut savoir que ce type de réponse est sanctionné et que l’absence d’argument ou le manque de précision rend la réponse irrecevable.
Pour terminer ce paragraphe, il reste toujours un noyau de candidats qui ne peuvent s’empêcher de faire du remplissage au lieu d’argumenter face aux questions dont le résultat est donné (exercice 2) : ceci est vécu comme une fraude (mot utilisé par plusieurs correcteurs).
Rappelons, une fois encore, que l’honnêteté, la simplicité, la précision et la rigueur sont des vertus attendues par tous les correcteurs sans exception, et qu’une bonne réponse est toujours une réponse construite rigoureusement.
La correction dématérialisée s’est très bien déroulée et il ne faut noter que très peu de problèmes de numérisation, tous très vite résolus par le service compétent.
