Aujourd’hui, focus sur un classique des exercices de probabilité, j’ai nommé : la loi logistique standard.
Présentation
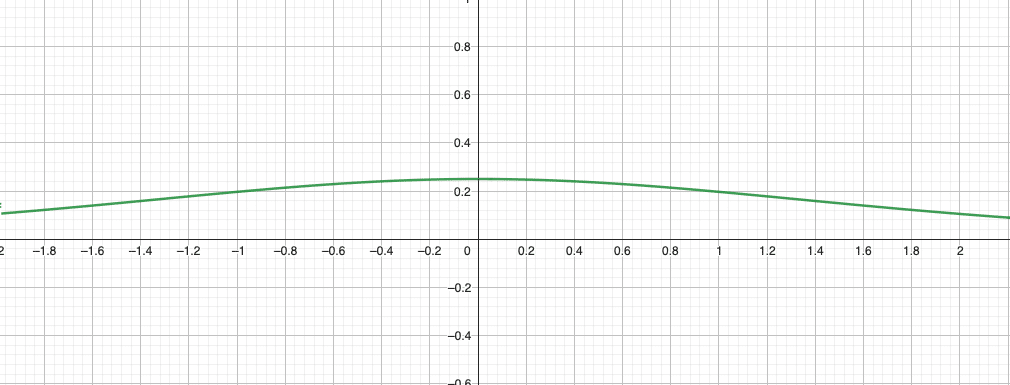
On dit que la variable aléatoire \(X\) suit la loi logistique standard si elle admet pour densité la fonction f définie sur \(\mathbb{R}\) par \(\forall x \in \mathbb R, f(x)=\frac{e^{-x}}{(1+e^{-x})^2}\)
La courbe de la fonction de densité peut être représentée ainsi :
La fonction de répartition est donnée par \(\forall x \in \mathbb R, \Lambda(x)=\frac{1}{1+e^{-x}}\)
Espérance et variance
\(X\) admet une espérance et une variance qui valent respectivement 0 et \(\frac{\pi^2}{3}\)
On trouve ces résultats par le calcul.
Loi logistique
Pour tout couple \((r,s)\in \mathbb{R} \times \mathbb{R}_{+}^{*}\), on dit qu’une variable aléatoire \(Y\) suit la loi logistique \(\mathcal{L}(r,s)\) si la variable aléatoire \(Z=\frac{Y-r}{s}\) suit la loi logistique standard.
Loi exponentielle
La loi logistique est intéressante, car elle te permet de faire le lien avec deux variables suivant une loi exponentielle de paramètre 1.
Montrons ainsi que si on pose \(U_1\) et \(U_2\) deux variables indépendantes suivant chacune une loi exponentielle de paramètre 1, alors \(ln(\frac{U_1}{U_2})\) suit la loi logistique standard.
Démonstration
\(Z=ln(U_1)-ln(U_2)\). On a :
\(\forall x \in \mathbb R, P(ln(U_1) \le x)=P(U_1\le e^{-x})=1-exp(-e^x)\)
On en déduit une densité de \(ln(U_1)\) en dérivant sa fonction de répartition qui est bien \(C^1\) sur \(\mathbb{R}\) : \(\forall x \in \mathbb R, f_{ln(U_1)}(x)=exp(x-e^x)\)
Quant à \(-ln(U_2)\), on trouve pour densité, \(f_{ln(U_2)}(x)=exp(-x-e^{-x})\)
D’après le lemme des coalitions, \(ln(U_1)\) et \(-ln(U_2)\) sont indépendants et comme la densité de \(ln(U_1)\) est bornée, on peut réaliser un produit de convolution pour trouver la loi de \(ln(U_1)-ln(U_2)\)
On a alors :
\(
\begin{align}
\forall x \in \mathbb R, h(x)&= \displaystyle \int_{-\infty}^{+\infty} f_{ln(U_1)}(x-t)f_{ln(U_2)}(t) \, \mathrm{d}t \\
&=\displaystyle \int_{-\infty}^{+\infty} exp(x-t-e^{x-t})exp(-t-e^{-t}) \, \mathrm{d}t \\
&=e^x\displaystyle \int_{-\infty}^{+\infty} e^{-2t}exp(-(1+e^x)e^{-t}) \, \mathrm{d}t
\end{align}
\)
On fait le changement de variable bijectif \(y=e^{-t}\). Il vient alors :
\(h(x)=e^x\displaystyle \int_{0}^{+\infty} yexp(-(1+e^x)y)\, \mathrm{d}t\)
En s’appuyant sur l’espérance de \(\mathcal{E}(1+e^x)\), on aboutit à \(\forall x \in \mathbb R, h(x)=\frac{e^x}{(1+e^x)^2}=\frac{e^{-x}}{(1+e^{-x})^2}\)
On a donc le résultat escompté.
Sujets d’annales
Voici une liste d’annales où tu peux retrouver cette notion. Fais ton choix et applique-toi à rédiger. C’est un très bon entraînement !
Tu peux retrouver toutes les autres ressources en mathématiques juste ici.