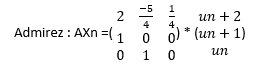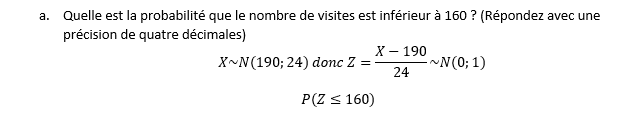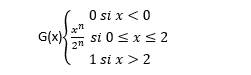Ça y est ! Vous connaissez toutes les formules indispensables par cœur et vous vous dites que ce n’était finalement pas si difficile que ça, et vous avez bien raison. Pour autant, le 20 à l’ESCP est encore loin d’être dans la poche, même celui d’ESC ou d’ECRICOME. Pour l’instant, vous disposez seulement (si vos connaissances actuelles en mathématiques s’arrêtent aux formules de l’article précédent, ce qui serait quand même dommage mais bon, il n’est pas encore trop tard pour se rattraper) des outils qui vous permettront de répondre correctement aux simples questions de cours (vous êtes incollable sur les formules d’espérance de n’importe quelle loi de probabilité discrète ou continue maintenant j’espère) et qui sont indispensables pour les questions nécessitant une démonstration, un raisonnement ou un peu de logique et d’observation. C’est pourquoi nous allons maintenant aborder ce qui caractérise le plus, selon moi, l’épreuve de maths en ECT : les fameuses questions qui retombent ABSOLUMENT tout le temps. Car oui, en plus de présenter une difficulté loin d’être insurmontable, les problèmes et les questions qui sont posés ont également le bon goût de grandement se ressembler chaque année. On pourrait presque croire que les concepteurs reprennent à chaque fois le même énoncé avec une matrice et une fonction différentes. Bon, il ne faut pas non plus exagérer, les questions ne seront pas toutes parfaitement identiques. De fait, celles qui le sont représentent une véritable opportunité qu’il faut savoir saisir car ce sont littéralement des points donnés à n’importe quel élève qui aura travaillé les maths pendant sa prépa.
Matrices :
Avant de commencer, ce qu’il faut bien comprendre pour pouvoir réussir la partie sur les matrices, c’est que TOUS les calculs, tous les résultats, toutes les informations de l’énoncé serviront pour plus tard, et notamment pour les récurrences. Si on vous demande de calculer 4A-6B ou de faire P*Q, ce n’est pas juste pour vous donner des points et éviter qu’un trop grand nombre de candidats aient 1/20 (enfin si un peu mais bon, il ne faut pas le dire). Cela a pour but de vous faire remarquer une relation qui vous servira forcément dans une des questions suivantes, en vérifiant une relation de récurrence faisant intervenir des suites par exemple. D’ailleurs, je vous précise que pour rédiger la partie matrice, je me suis surtout basé sur les sujets ESCP 2015 et 2016 où les parties matrices ne pouvaient être plus classiques que dans ces deux sujets (et ce sont les deux derniers sujets qui sont tombés donc on peut légitimement penser que la tendance de proposer un exercice de matrice très abordables se poursuivra), et la première question consiste simplement à faire des opérations basiques dans l’un, et de lire l’énoncé dans l’autre. Quand je vous dis que tout sert pour plus tard !
Le raisonnement sera toujours le même. Dans la première partie de la question, vous prenez votre matrice et vous la multiplier par Xn pour obtenir Xn+1 et dans la deuxième, vous citez votre hypothèse de récurrence ainsi que la relation que vous venez de justifier et le tour est jouer.
4] Cas d’une chaîne de Markov :
Parfois, l’exercice de diagonalisation d’une matrice est utilisé dans le cadre d’une chaîne de Markov (cela se reconnaît facilement, il y a une partie B avec trois tonnes de textes qui vous explique que si Jean-Kevin achète un dessert A cette semaine, alors il achètera le B avec la probabilité 1/3 et le C avec la probabilité 1/7 la semaine suivante) donc en plus des questions précédemment citées, vous retrouverez alors en plus ces deux questions (sachant que vous pouvez également les retrouver dans la partie probabilités discrètes) :
Ensuite, il faut reconduire le même raisonnement mais dans l’éventualité où il a choisi le dessert B puis le C (c’est pour cela qu’on additionne). Lorsque vous avez écrit votre grosse formule, vous n’avez plus qu’à remplacer par les données de l’énoncé et faire de même pour P(Bn+1) et P(Cn+1).
5] Questions très probables sur la recherche de valeurs propres et de vecteurs propres :
Faisant partie des nouveautés du programme depuis 2016, on ne peut pas se baser sur les anciens sujets pour pouvoir affirmer que telle ou telle question tombera. Mais rien qu’avec les sujets 2016, on peut déjà dresser un tableau de toutes les éventualités.
Vous n’avez alors plus qu’à résoudre : par exemple, pour la première ligne, on voit très bien que pour que cela fasse 0, on doit prendre un chiffre et faire moins ce même chiffre donc 1 et -1. Puisqu’on a décidé que z=0, pour vérifier l’équation de la deuxième ligne on prend y=1 et on vérifie bien que la dernière ligne soit vraie. On a bien 1+1+2*(-1)=0
6] Rappel sur les suites :
De nombreuses fois, l’exercice sur les matrices fera appel à des suites. Il est alors essentiel de connaître les bases :
Suite arithmétique : un = u0 +n*r (exemple : u0 = 200 et de raison -3 alors un = 200 + n*(-3))
Attention si le premier terme est u1 alors on a un = 200 + (n-1)*(-3)
Suite géométrique : un = u0*q^n (exemple : u0 = 500 et de raison 1/5 alors un = 500*(1/5)^n
Même chose si le premier terme est u1 un = 500*(1/5)^n-1
Etude de fonctions et suites :
1] Limites, dérivée, et tableau de variation :
Les sujets sont obligés de vous faire passer par cette étape puisque ce sont les renseignements indispensables pour pouvoir avoir une idée de ce à quoi ressemble votre courbe. Rater ces premières questions revient donc à rater l’exercice dans son intégralité. Mais cela n’arrivera pas puisque maintenant, vous connaissez toutes vos limites, vos théorèmes de croissance comparé et toutes vos dérivées. De fait, toutes les petites questions jusqu’à celle qui vous demandera de tracer la courbe ne seront que du gâteau. Pensez bien à dire lorsque vous serez au tableau de variation que les variations de la courbe sont données par le signe de sa dérivée pour valoriser votre copie. Je vous rajoute aussi la formule pour déterminer une tangente en un point d’abscisse que j’avais oublié de vous donner la dernière fois.
La logique sera toujours la même, donc si malheureusement vous n’arrivez pas à la saisir, je peux ne vous conseiller que d’apprendre par cœur les réponses, même si ça va être dur et barbant.
Probabilités discrètes :
Bon alors là, vous allez pouvoir vous faire plaisir et ressortir toutes les formules de probabilité, d’espérance et de variance que vous avez appris et même celle du biais et du risque quadratique d’un estimateur. Mais avant de recracher tout votre cours, il vous faut justifier CORRECTEMENT pourquoi la situation que l’on vous décrit suit telle ou telle loi et c’est justement cette rédaction que nous allons voir.
1] Cas d’une loi binomiale :
On procède à une expérience qui suit un schéma de Bernoulli consistant à effectuer un tirage parmi un échantillon de x objets et on considère comme succès de l’expérience l’évènement « l’objet tiré fonctionne » de probabilité 0.3 et comme échec l’évènement « l’objet tiré ne fonctionne pas » de probabilité 0.7. On répète n fois cette expérience de Bernoulli, chaque tirage étant effectué de manière IDENTIQUE ET INDEPENDANTE. Soit X la variable aléatoire comptant le nombre de fois où l’évènement « l’objet tiré fonctionne » se réalise, X suit donc une loi BINOMIALE de paramètres p = 0.3 et n = n
2] Cas d’une loi géométrique :
On procède à une expérience qui suit un schéma de Bernoulli consistant à effectuer un tirage parmi un échantillon de x objets et on considère comme succès de l’expérience l’évènement « l’objet tiré fonctionne » de probabilité 0.3 et comme échec l’évènement « l’objet tiré ne fonctionne pas » de probabilité 0.7. On répète cette expérience de Bernoulli, chaque tirage étant effectué de manière IDENTIQUE ET INDEPENDANTE, jusqu’à ce que pour LA PREMIERE FOIS l’évènement « l’objet tiré fonctionne » se réalise. Soit X la variable aléatoire comptant le nombre de tirage nécessaire avant que cet évènement ne se réalise pour la première fois, X suit donc une loi géométrique de paramètres p = 0.3 et 1-p = 0.7.
3] Cas d’une loi de Poisson :
Cette fois, aucune rédaction puisque vous n’avez pas à identifier la loi de Poisson. Ce sera l’énoncé qui vous dira que l’on peut approcher la loi par la loi de Poisson. Vous devrez alors simplement lire la table en prenant le bon paramètre. Par exemple, si votre loi que vous cherchez à estimer par la loi de Poisson avait pour espérance 3, le paramètre à utiliser pour lire la table sera 3. Pour le reste des questions, vous connaissez vos formules.
4] Cas d’une loi normale :
Là-aussi, pas de rédaction puisque c’est l’énoncé qui vous dit qu’on approche la loi par la loi Normale. Pour autant, s’il n’y a pas vraiment de formule à connaître, il faut savoir la démarche à suivre pour les 3 types de questions que l’on peut vous posez dans le cadre d’une loi normale, car ce sera toujours la même. Pour mieux comprendre les explications, cherchez la table des z de la loi normale sur internet.
Supposez que les visites sur le site internet de votre entreprise, entre midi et 13h en semaine, suit (approximativement) une loi normale avec une moyenne de 190 et un écart-type de 24. Pour les questions qui suivent, utilisez la table des Z :
Probabilités continues :
Les densités de probabilités semblent l’exercice le plus difficile au premier abord. Pourtant, c’est cette partie-là est quasiment identique d’année en année, même les fonctions utilisées sont quasiment toujours pareil (si vous savez primitiver 1/x vous avez gagné). La preuve, je vais me
3] Définition d’une nouvelle variable aléatoire à partir de la première variable aléatoire :
Le but sera d’abord de trouver la fonction de répartition de cette variable aléatoire afin, ensuite, de donner la densité de cette nouvelle variable aléatoire en dérivant cette fonction de répartition, en sachant que, bien souvent, on remarquera que la fonction de répartition de la nouvelle variable aléatoire correspond à celle d’une loi exponentielle ou uniforme et qu’on aura plus qu’à appliquer le cours pour donner la densité, l’espérance et la variance de cette nouvelle loi (on fait donc le chemin inverse).
U = X² et Y = U/4
Et là, vous dérivez cette fonction de répartition pour obtenir la densité mais si vous savez bien vos formules, vous avez déjà reconnu la fonction de répartition d’une loi uniforme mais dérivez la fonction de répartition pour être sûr, puis donner l’espérance et la variance.
4] Zn = sup(X1, X2, X3….Xn) :
Vous venez de vous farcir des tonnes de calculs et de justifications bien lourdingues et pourtant l’exercice veut vous embêter (restons poli) une dernière en créant une dernière variable aléatoire qui ressemble à rien à première vue. En réalité, ce Zn correspond au maximum que la variable aléatoire peut prendre comme valeur en répétant n fois la variable aléatoire X. Ce Zn, l’énoncé va vous le traduire (enfin normalement, donc s’il ne le fait pas vaut mieux le savoir) par :
Et l’énoncé terminera sûrement par vous demander de donner la densité de Zn (rappelez-vous : il n’y a qu’à dériver la fonction de répartition) et de donner son espérance.
Et voilà, désormais, vous avez toutes les armes en main pour rouler sur n’importe quel sujet de maths. Vous avez toutes les formules, vous savez comment rédiger les questions qui tomberont à coup sûr, il n’y a plus qu’à attendre votre heure de gloire. Alors mettons les choses au clair, je ne vous dis pas qu’avec tout cela, vous serez en mesure de répondre à absolument toutes les questions sans réfléchir, loin de là. Et là, je vous entends déjà crier au putaclique en gueulant « T’avais promis le 20/20 en maths » sauf que dans les faits, même sans répondre à toutes les questions, les deux articles permettent quand même de s’en rapprocher énormément. Déjà, je rappelle que l’ESCP accorde le 20 aux alentours de 75%-80% du sujet traité correctement et avec tout ce que je vous ai donné, vous pouvez facilement faire 50% à 60% du sujet sans faute donc vous serez bien capable de faire 10% par vous-même j’espère. Ensuite, n’oubliez pas une chose : c’est un concours ! Et en répondant à toutes ces questions, vous sortirez facilement de l’énorme lot de candidats qui auront abandonné les maths en prépa et qui seront sortis de la salle au bout de 2h. Vous serez donc considérez au minimum comme une bonne copie qui a pris soin de bien rédiger et justifier chaque réponse que vous avez été capable d’apporter et votre copie sera donc valorisée. Donc, si avec tous ces facteurs, vous ne décrochez une super note au concours, c’est (presque) que vous l’aurez fait exprès. Pour finir, je tiens juste à préciser que je n’ai pas abordé scilab tout simplement parce que c’est nouveau et les questions possibles sont beaucoup trop vastes par rapport aux estimateurs ou à la recherche de valeur propre et de vecteur propre par exemple donc je ne préfère pas vous dire de bêtise. Surtout, je n’ai cessé de dire que les sujets étaient presque identiques d’année en année et se simplifier à chaque fois. Seulement voilà, après des années à désespérer devant un niveau beaucoup trop inégal en mathématique dans notre filière, les correcteurs des sujets 2016 ont déclaré, pour une fois, dans leur rapport avoir été agréablement surpris par le bon niveau des candidats n’ayant alors pas hésité à monter la barre à 80% du sujet traité pour décrocher le 20. C’est pourquoi une complexification des sujets est peut-être à attendre pour les sujets 2017 (ou pas ?).